Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

[4] Trong không gian \(Oxyz\), cho đường thẳng \(\Delta \) đi qua \(E\left( {1 + 3a; – 2;2 + 3a} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {a;1;a + 1} \right)\). Biết khi \(a\) thay đổi luôn tồn tại một mặt cầu \(\left( S \right)\) cố định có tâm \(I\left( {m;n;p} \right)\) bán kính \(R\) đi qua điểm \(M\left( {1;1;1} \right)\) và tiếp xúc với đường thẳng \(\Delta \). Một khối nón \(\left( N \right)\) có đỉnh \(I\) và đường tròn đáy của khối nón nằm trên mặt cầu \(\left( S \right)\). Thể tích lớn nhất của khối nón \(\left( N \right)\) là \(\max {V_{\left( N \right)}} = \frac{{q\pi }}{3}\). Khi đó tổng \(m + n + p + q\) bằng

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:,

[4] Trong không gian \(Oxyz\), cho đường thẳng \(\Delta \) đi qua \(E\left( {1 + 3a; - 2;2 + 3a} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {a;1;a + 1} \right)\). Biết khi \(a\) thay đổi luôn tồn tại một mặt cầu \(\left( S \right)\) cố định có tâm \(I\left( {m;n;p} \right)\) bán kính \(R\) đi qua điểm \(M\left( {1;1;1} \right)\) và tiếp xúc với đường … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho đường thẳng \(\Delta \) đi qua \(E\left( {1 + 3a; – 2;2 + 3a} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {a;1;a + 1} \right)\). Biết khi \(a\) thay đổi luôn tồn tại một mặt cầu \(\left( S \right)\) cố định có tâm \(I\left( {m;n;p} \right)\) bán kính \(R\) đi qua điểm \(M\left( {1;1;1} \right)\) và tiếp xúc với đường thẳng \(\Delta \). Một khối nón \(\left( N \right)\) có đỉnh \(I\) và đường tròn đáy của khối nón nằm trên mặt cầu \(\left( S \right)\). Thể tích lớn nhất của khối nón \(\left( N \right)\) là \(\max {V_{\left( N \right)}} = \frac{{q\pi }}{3}\). Khi đó tổng \(m + n + p + q\) bằng

[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). Khi \(\left( N \right)\) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của \(\left( N \right)\) có phương trình là \(x + ay + bz + c = 0\). Giá trị của \(a + b + c\) bằng

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:,

[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). Khi \(\left( N \right)\) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của \(\left( N \right)\) có phương trình là \(x + ay + bz + c = 0\). Giá trị của \(a + b + c\) bằng

Cho đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C’} \right)\)và ngược lại tâm \(O’\) của \(\left( {C’} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) quay quanh đường \(OO’\)tạo ra hai mặt cầu \(\left( S \right),\,\left( {S’} \right)\) Tính thể tích \(V\) phần chung của hai khối cầu tạo bởi \(\left( S \right),\,\left( {S’} \right)\)là

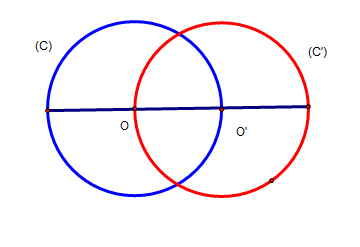
Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:, ,

Cho đường tròn \(\left( C \right)\) và \(\left( {C'} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C'} \right)\)và ngược lại tâm \(O'\) của \(\left( {C'} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C'} \right)\) quay quanh đường \(OO'\)tạo ra hai mặt cầu \(\left( S … [Đọc thêm...] vềCho đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C’} \right)\)và ngược lại tâm \(O’\) của \(\left( {C’} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) quay quanh đường \(OO’\)tạo ra hai mặt cầu \(\left( S \right),\,\left( {S’} \right)\) Tính thể tích \(V\) phần chung của hai khối cầu tạo bởi \(\left( S \right),\,\left( {S’} \right)\)là

Cho phương trình \({2^{\left( {x + 2} \right)\left( {2x + 1} \right)}}.\ln \left[ {2\left( {x + 2} \right)x + 3} \right] = {2^{y + {x^2} + x + 1}}.\ln \sqrt {{x^2} + y + 1} \) (1) với \(y \ge 0\). Khi \(2{x^2} – y\) đạt giá trị nhỏ nhất thì giá trị của biểu thức \(S = y – x\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:,

Cho phương trình \({2^{\left( {x + 2} \right)\left( {2x + 1} \right)}}.\ln \left[ {2\left( {x + 2} \right)x + 3} \right] = {2^{y + {x^2} + x + 1}}.\ln \sqrt {{x^2} + y + 1} \) (1) với \(y \ge 0\). Khi \(2{x^2} - y\) đạt giá trị nhỏ nhất thì giá trị của biểu thức \(S = y - x\) bằng A. \(16\). B. \(14\). C. \(10\).\(\) D. \(12\). Lời giải: (1)\( \Leftrightarrow … [Đọc thêm...] vềCho phương trình \({2^{\left( {x + 2} \right)\left( {2x + 1} \right)}}.\ln \left[ {2\left( {x + 2} \right)x + 3} \right] = {2^{y + {x^2} + x + 1}}.\ln \sqrt {{x^2} + y + 1} \) (1) với \(y \ge 0\). Khi \(2{x^2} – y\) đạt giá trị nhỏ nhất thì giá trị của biểu thức \(S = y – x\) bằng

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\,\,:\,\,{x^2}\, + \,{y^2} + \,{z^2}\, – \,\,8x\, + 6y\, + \,2z\,\, + 6\, = 0\)và mặt phẳng \(\left( P \right)\,\,:\,x\, – \,2y\, = \,\,0\). Có bao nhiệu điểm \(M\)có tọa độ nguyên nằm trên \(\left( P \right)\)sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\)qua \(M\)và vuông góc với nhau.

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:, ,

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\,\,:\,\,{x^2}\, + \,{y^2} + \,{z^2}\, - \,\,8x\, + 6y\, + \,2z\,\, + 6\, = 0\)và mặt phẳng \(\left( P \right)\,\,:\,x\, - \,2y\, = \,\,0\). Có bao nhiệu điểm \(M\)có tọa độ nguyên nằm trên \(\left( P \right)\)sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\)qua \(M\)và vuông góc với nhau. A. … [Đọc thêm...] vềTrong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\,\,:\,\,{x^2}\, + \,{y^2} + \,{z^2}\, – \,\,8x\, + 6y\, + \,2z\,\, + 6\, = 0\)và mặt phẳng \(\left( P \right)\,\,:\,x\, – \,2y\, = \,\,0\). Có bao nhiệu điểm \(M\)có tọa độ nguyên nằm trên \(\left( P \right)\)sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\)qua \(M\)và vuông góc với nhau.

nbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

nbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là A. \(V = {a^3}\sqrt 3 \) B. \(V = \frac{{{a^3}\sqrt 3 }}{2}\) C. … [Đọc thêm...] vềnbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là

Cho lăng trụ tứ giác \(ABCD.A’B’C’D’\) có đáy là hình vuông và cạnh bên bằng \(2a\). Hình chiếu của \(A’\) lên mặt phẳng \(\left( {ABCD} \right)\)là trung điểm của \(AD\), đường thẳng \(A’C\) tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc là \({45^0}\). Thể tích khối lăng trụ\(ABCD.A’B’C’D’\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\) có đáy là hình vuông và cạnh bên bằng \(2a\). Hình chiếu của \(A'\) lên mặt phẳng \(\left( {ABCD} \right)\)là trung điểm của \(AD\), đường thẳng \(A'C\) tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc là \({45^0}\). Thể tích khối lăng trụ\(ABCD.A'B'C'D'\) bằng A. \(\frac{{16{a^3}}}{3}\). B. \(\frac{{8{a^3}\sqrt {30} … [Đọc thêm...] về

Cho lăng trụ tứ giác \(ABCD.A’B’C’D’\) có đáy là hình vuông và cạnh bên bằng \(2a\). Hình chiếu của \(A’\) lên mặt phẳng \(\left( {ABCD} \right)\)là trung điểm của \(AD\), đường thẳng \(A’C\) tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc là \({45^0}\). Thể tích khối lăng trụ\(ABCD.A’B’C’D’\) bằng

Cho hình lăng trụ \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A\), cạnh \(BC = 2a\) và

\(\widehat {ABC} = {60^0}\). Biết tứ giác \(BCC’B’\) là hình thoi có \(\widehat {B’BC}\) là góc nhọn, mặt phẳng \(\left( {BCC’B’} \right)\)vuông góc với \(\left( {ABC} \right)\), góc giữa hai mặt phẳng \(\left( {ABB’A’} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Thể tích khối lăng trụ \(ABC.A’B’C’\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\), cạnh \(BC = 2a\) và \(\widehat {ABC} = {60^0}\). Biết tứ giác \(BCC'B'\) là hình thoi có \(\widehat {B'BC}\) là góc nhọn, mặt phẳng \(\left( {BCC'B'} \right)\)vuông góc với \(\left( {ABC} \right)\), góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Thể … [Đọc thêm...] vềCho hình lăng trụ \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A\), cạnh \(BC = 2a\) và

\(\widehat {ABC} = {60^0}\). Biết tứ giác \(BCC’B’\) là hình thoi có \(\widehat {B’BC}\) là góc nhọn, mặt phẳng \(\left( {BCC’B’} \right)\)vuông góc với \(\left( {ABC} \right)\), góc giữa hai mặt phẳng \(\left( {ABB’A’} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Thể tích khối lăng trụ \(ABC.A’B’C’\) bằng