Một vật dụng bằng sắt đang nằm trên mặt sàn có tay cầm dài $58$ cm nối với một ống trụ dày $4$ cm và có đường kính đáy bằng $30$ cm. Nếu không giữ thì sẽ luôn có một lực làm vật rung động, đề vật đứng yên thì người ta đã nối một đoạn đây từ điểm $B$ (là một điểm nằm trên đường tròn chính giữa của ống trụ to) đến điểm $C$ nằm trên bờ tường. Trên hệ trục ${O x y z}$, xét gốc tọa độ là điểm gắn ống trụ với bờ tuờng, bờ tường là mặt phẳng ( ${O x z}$ ), trục ${O y}$ là trục của hình trụ, điểm $A$ nằm chính giữa ống trụ to, điểm $B$ có hoành độ âm, cao độ dương và ${A B}$ tạo với trục ${O z}$ một góc $30$ độ, các số liệu được cho như hình vẽ, đơn vị trên các hệ trục tính theo cm. Biết rằng lực căng $\vec{T}$ trên đoạn dây ${B C}$ có độ lớn bằng $500$ N.
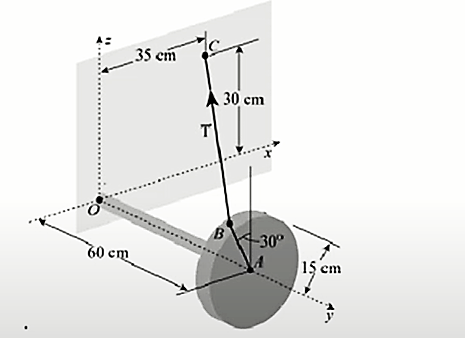
a) Hình chiếu của $C$ lên mặt phẳng ${(O x y)}$ có tọa độ là ${(35 ; 0 ; 0)}$.
b) Góc giữa đường thẳng ${A B}$ và mặt phăng ${(O x y)}$ bằng $30^{\circ}$.
c) Vectơ $\overrightarrow{BC}$ có tọa độ $(a ; b ; c)$. Khi đó $2 a-b=40$.
d) Vectơ lực tác dụng lên đoạn dây ${B C}$ có hoành độ là $120$ (làm tròn kết quả đến hàng đơn vị theo Newton).
Lời giải:
(Đúng) Hình chiếu của $C$ lên mặt phẳng ${(O x y)}$ có tọa độ là ${(35 ; 0 ; 0)}$.
(Vì): Đúng. Ta có $C(35 ; 0 ; 30)$. Suy ra hình chiếu của $C$ lên mặt phẳng $(O x y)$ có toạ độ là $(35 ; 0 ; 0)$.
(Sai) Góc giữa đường thẳng ${A B}$ và mặt phăng ${(O x y)}$ bằng $30^{\circ}$.
(Vì): Sai. Theo giả thiết, ta có $(A B, O z)=30^{\circ}$. Mà $O z \perp(O x y)$, suy ra $(A B,(O x y))=90^{\circ}-30^{\circ}=60^{\circ}$.
(Sai) Vectơ $\overrightarrow{BC}$ có tọa độ $(a ; b ; c)$. Khi đó $2 a-b=40$.
(Vì): Sai. +) Vì $d(B,(O x z))=O A=60$. Suy ra tung độ của điểm $B$ bằng 60. +) Gọi $H$ là hình chiếu của $B$ lên mặt phẳng $(O x y)$.
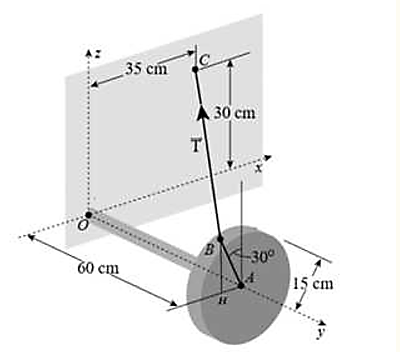
Xét tam giác vuông ${B H A}$, ta có: $\cos \widehat{B A H}=\dfrac{A H}{A B}$ $\Rightarrow A H=A B \cdot \cos \widehat{B A H}=15 \cdot \cos 60^{\circ}=\dfrac{15}{2}$ Suy ra hoành độ của điểm $B$ bẳng $-\dfrac{15}{2}$. +) Ta có $B H=\sqrt{A B^2-A H^2}=\dfrac{15 \sqrt{3}}{2}$. Suy ra cao độ của điểm $B$ bằng $\dfrac{15 \sqrt{3}}{2}$. Suy ra $B\left(-\dfrac{15}{2} ; 60 ; \dfrac{15 \sqrt{3}}{2}\right)$. Suy ra $\overrightarrow{B C}\left(\dfrac{85}{2} ;-60 ; 30-\dfrac{15 \sqrt{3}}{2}\right)$. $\Rightarrow 2 a-b=145$
(Sai) Vectơ lực tác dụng lên đoạn dây ${B C}$ có hoành độ là $120$ (làm tròn kết quả đến hàng đơn vị theo Newton).
(Vì): Sai. Nhắc lại: Nếu 2 vectơ $\vec{u}, \bar{v}$ cùng hướng thì suy ra $\vec{u}=\dfrac{|\vec{u}|}{|\vec{v}|}\cdot \overrightarrow{v}$ Vì $\overrightarrow{T}$ là vectơ lực tác dụng lên đoạn dây $BC$ nên $\vec{T}$ cùng hướng với $\overrightarrow{B C}$. Áp dụng cho $2 \text { vecto } \vec{T}, \overrightarrow{B C}$ ta có $\vec{T}=\dfrac{|\vec{T}|}{|\overrightarrow{B C}|} \cdot \overrightarrow{B C}$ $=\dfrac{500}{\sqrt{\left(\dfrac{85}{2}\right)^2+(-60)^2+\left(30-\dfrac{15 \sqrt{3}}{2}\right)^2}} \cdot\left(\dfrac{85}{2} ;-60 ; 30-\dfrac{15 \sqrt{3}}{2}\right)$ $\Rightarrow x_{\vec{T}}=\dfrac{500}{75,47} \cdot \dfrac{85}{2} \approx 282(\mathrm{N}) .$
(Đúng) Hình chiếu của $C$ lên mặt phẳng ${(O x y)}$ có tọa độ là ${(35 ; 0 ; 0)}$.
(Sai) Góc giữa đường thẳng ${A B}$ và mặt phăng ${(O x y)}$ bằng $30^{\circ}$.
(Sai) Vectơ $\overrightarrow{BC}$ có tọa độ $(a ; b ; c)$. Khi đó $2 a-b=40$.
(Sai) Vectơ lực tác dụng lên đoạn dây ${B C}$ có hoành độ là $120$ (làm tròn kết quả đến hàng đơn vị theo Newton).
