Một chiếc đèn trang trí (gồm các bóng đèn gắn vào một giá hình tròn) như hình bên dưới. Đèn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm $O$ trên trần nhà và lần lượt buộc vào ba điểm $A,B,C$ trên giá sao cho tam giác $ABC$ đều. Độ dài của ba đoạn dây $OA,OB,OC$ đều bằng $L$, trọng lượng của chiếc đèn là $27N$, bán kính của giá hình tròn là $0,5m$.

Biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là $12N$. Hỏi chiều dài tối thiểu của mỗi sợi dây là bao nhiêu mét? (kết quả làm tròn đến hàng phần trăm).
Lời giải
Đáp án: $0,76$.
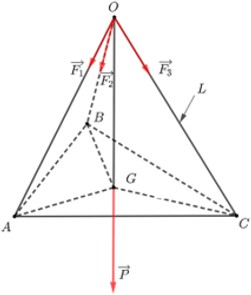
Gọi $G$ là trọng tâm tam giác $ABC$. Vì tam giác $ABC$ đều nên $G$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Do đó, $GA=GB=GC=0,5m$. Gọi $F$ là độ lớn của các lực căng ${{F}_{1}},{{F}_{2}},{{F}_{3}}$ trên mỗi sợi dây. Khi đó, $F=F\left( L \right)$ là một hàm số với biến số là L.
Theo bài ra ta có $OA=OB=OC=L$ nên $OG\bot \left( ABC \right)$ và $\left| \overrightarrow{OA} \right|=\left| \overrightarrow{OB} \right|=\left| \overrightarrow{OC} \right|=L$
Do đó, $\left| \overrightarrow{{{F}_{1}}} \right|=\left| \overrightarrow{{{F}_{2}}} \right|=\left| \overrightarrow{{{F}_{3}}} \right|$. Vì vậy tồn tại hằng số $c\ne 0$ sao cho $\overrightarrow{{{F}_{1}}}=c\overrightarrow{OA}, \overrightarrow{{{F}_{2}}}=c\overrightarrow{OB}, \overrightarrow{{{F}_{3}}}=c\overrightarrow{OC}$.
Suy ra $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=c\left( \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} \right)=3c\overrightarrow{OG}$.
Mặt khác, ta lại có $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=\overrightarrow{P}$ với $\overrightarrow{P}$ là trọng lực tác dụng lên chiếc đèn.
Mà trọng lực tác dụng lên chiếc đèn là $27N$ nên $\left| \overrightarrow{P} \right|=27\Leftrightarrow 3c\left| OG \right|=27N\Leftrightarrow c=\dfrac{9}{OG}$.
Tam giác $AOG$ vuông tại $G$ (do $OG\bot \left( ABC \right)$ ) nên ta suy ra $OG=\sqrt{O{{A}^{2}}-G{{A}^{2}}}=\sqrt{{{L}^{2}}-0,{{5}^{2}}} \left( m \right)$ với $L{>}0,5$.
Do đó, $OG=\sqrt{{{L}^{2}}-0,{{5}^{2}}} \Rightarrow c=\dfrac{9}{\sqrt{{{L}^{2}}-0,{{5}^{2}}}}$.
Khi đó, $\left| \overrightarrow{F} \right|=\left| \overrightarrow{{{F}_{1}}} \right|=c\left| OA \right|=\dfrac{9L}{\sqrt{{{L}^{2}}-0,{{5}^{2}}}}$ (với $L{>}0,5$ ).
Ta có lực căng tối đa của mỗi sợi dây là $12N$.
Suy ra $F\left( L \right)\le 12\Leftrightarrow \dfrac{9L}{\sqrt{{{L}^{2}}-0,{{5}^{2}}}}\le 12$ $\Leftrightarrow 3L\le 4\sqrt{{{L}^{2}}-0,{{5}^{2}}}$ $\Leftrightarrow 9{{L}^{2}}\le 16{{L}^{2}}-4$ $\Leftrightarrow 7{{L}^{2}}\ge 4$ $\Rightarrow L\ge \dfrac{2\sqrt{7}}{7}$. Vậy chiều dài tối thiểu của mỗi sợi dây là $\dfrac{2\sqrt{7}}{7}\approx 0,76$ (m).
