Hình học không gian

Đề bài: Cắt tứ diện $ABCD$ bằng một mặt phẳng $(P)$ trong mỗi trường hợp sau đây:a)$(P)$ song song với $BD$, đi qua $M, N$ là hai điểm lần lượt nằm trên hai cạnh $AB$ và $BC$.b) $(P)$ qua $M$ nằm trên cạnh $AB$ và song song với hai đường thẳng $BD, AC$.c) $(P)$ song song với $BD$ và $AC$, ngoài ra (P) đi qua $M$ thuộc đoạn $AB$ sao cho $\frac{AM}{MB}=\frac{AC}{BD}. $Xác định tính chất của thiết diện nhận được trong từng trường hợp nói trên.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he song song

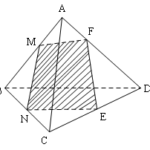
Đề bài: Cắt tứ diện $ABCD$ bằng một mặt phẳng $(P)$ trong mỗi trường hợp sau đây:a)$(P)$ song song với $BD$, đi qua $M, N$ là hai điểm lần lượt nằm trên hai cạnh $AB$ và $BC$.b) $(P)$ qua $M$ nằm trên cạnh $AB$ và song song với hai đường thẳng $BD, AC$.c) $(P)$ song song với $BD$ và $AC$, ngoài ra (P) đi qua $M$ thuộc đoạn $AB$ sao cho $\frac{AM}{MB}=\frac{AC}{BD}. $Xác định … [Đọc thêm...] vềĐề bài: Cắt tứ diện $ABCD$ bằng một mặt phẳng $(P)$ trong mỗi trường hợp sau đây:a)$(P)$ song song với $BD$, đi qua $M, N$ là hai điểm lần lượt nằm trên hai cạnh $AB$ và $BC$.b) $(P)$ qua $M$ nằm trên cạnh $AB$ và song song với hai đường thẳng $BD, AC$.c) $(P)$ song song với $BD$ và $AC$, ngoài ra (P) đi qua $M$ thuộc đoạn $AB$ sao cho $\frac{AM}{MB}=\frac{AC}{BD}. $Xác định tính chất của thiết diện nhận được trong từng trường hợp nói trên.

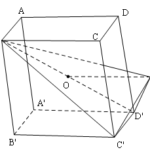
Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ với tâm $O$ và $AB=a, AD=b, AA'=c.$Với mọi điểm $M$ ta đặt $T=MA^2+MB^2+MC^2+MD^2+MA'^2+MB'^2+MC'^2+MD'^2$Chứng minh rằng $T=8MO^2+2(a^2+b^2+c^2)$. Hãy xác định vị trí của điểm $M$ để $T$ đạt giá trị bé nhất.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ với tâm $O$ và $AB=a, AD=b, AA'=c.$Với mọi điểm $M$ ta đặt $T=MA^2+MB^2+MC^2+MD^2+MA'^2+MB'^2+MC'^2+MD'^2$Chứng minh rằng $T=8MO^2+2(a^2+b^2+c^2)$. Hãy xác định vị trí của điểm $M$ để $T$ đạt giá trị bé nhất. Lời giải Theo công thức tính độ dài trung tuyến lần lượt trong các tam giác … [Đọc thêm...] vềĐề bài: Cho hình hộp $ABCD.A'B'C'D'$ với tâm $O$ và $AB=a, AD=b, AA'=c.$Với mọi điểm $M$ ta đặt $T=MA^2+MB^2+MC^2+MD^2+MA'^2+MB'^2+MC'^2+MD'^2$Chứng minh rằng $T=8MO^2+2(a^2+b^2+c^2)$. Hãy xác định vị trí của điểm $M$ để $T$ đạt giá trị bé nhất.

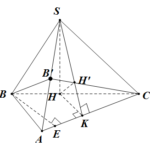
Đề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông tại $B; AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3};\widehat{SBC}=30^0$. Tìm khoảng cách từ $B$ đến mặt phẳng $(SAC)$.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông tại $B; AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3};\widehat{SBC}=30^0$. Tìm khoảng cách từ $B$ đến mặt phẳng $(SAC)$. Lời giải Kẻ $BE \bot AC, HK \bot AC \Rightarrow BE //HK$ Ta có : $SK \bot AC$(định lí ba đường vuông góc) $\Rightarrow AC \bot (SHK) … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác $S.ABC$ đáy là tam giác vuông tại $B; AB=3a, BC=4a$. Biết rằng mặt phẳng $(SBC)$ vuông góc với $(ABC)$. Giả sử $SB=2a\sqrt{3};\widehat{SBC}=30^0$. Tìm khoảng cách từ $B$ đến mặt phẳng $(SAC)$.

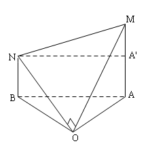
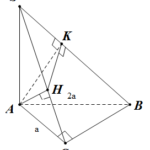
Đề bài: Trong mặt phẳng $(P)$ cho tam giác $OAB$, cân tại đỉnh $O,OA=a$ và cạnh đáy $AB=a\sqrt{3} $.Trên các đường thẳng $Ax\bot (P),By\bot (P)$ với $Ax,By$ nằm cùng phía đối với mặt phẳng $(P)$, ta lấy theo thứ tự, hai điểm $M,N$ sao cho $AM=a,BN=\frac{a}{2} $$a.$ Chứng minh tam giác $OMN$ vuông$b.$ Tính góc hợp bởi mặt phẳng $(OMN),(P)$

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Trong mặt phẳng $(P)$ cho tam giác $OAB$, cân tại đỉnh $O,OA=a$ và cạnh đáy $AB=a\sqrt{3} $.Trên các đường thẳng $Ax\bot (P),By\bot (P)$ với $Ax,By$ nằm cùng phía đối với mặt phẳng $(P)$, ta lấy theo thứ tự, hai điểm $M,N$ sao cho $AM=a,BN=\frac{a}{2} $$a.$ Chứng minh tam giác $OMN$ vuông$b.$ Tính góc hợp bởi mặt phẳng $(OMN),(P)$ Lời giải $a.$ Tính … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho tam giác $OAB$, cân tại đỉnh $O,OA=a$ và cạnh đáy $AB=a\sqrt{3} $.Trên các đường thẳng $Ax\bot (P),By\bot (P)$ với $Ax,By$ nằm cùng phía đối với mặt phẳng $(P)$, ta lấy theo thứ tự, hai điểm $M,N$ sao cho $AM=a,BN=\frac{a}{2} $$a.$ Chứng minh tam giác $OMN$ vuông$b.$ Tính góc hợp bởi mặt phẳng $(OMN),(P)$

Đề bài: Chứng minh rằng nếu ba đường thẳng phân biệt cắt nhau từng đôi một thì chúng đồng quy hoặc cùng nằm trong một mặt phẳng

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he song song

Đề bài: Chứng minh rằng nếu ba đường thẳng phân biệt cắt nhau từng đôi một thì chúng đồng quy hoặc cùng nằm trong một mặt phẳng Lời giải Với ba đường thẳng phân biệt $a,b,c$.Giả sử :$a\cap b=\left\{ {A} \right\} ,b\cap c=\left\{ {B} \right\} ,c\cap a=\left\{ {C} \right\} $Xét hai trường hợp :*Trường hợp $1:$ Ba điểm $A,B,C$ là ba điểm phân biệt.Do $a,b,c$ phân biệt … [Đọc thêm...] vềĐề bài: Chứng minh rằng nếu ba đường thẳng phân biệt cắt nhau từng đôi một thì chúng đồng quy hoặc cùng nằm trong một mặt phẳng

Đề bài: Trong mặt phẳng $(P)$ cho tam giác $ABC$ vuông tại $C, AB=2a,\widehat{CAB}=60^0$, đoạn $SA=h$ và $SA$ vuông góc với $(P)$. Tìm $h$ sao cho góc giữa hai mặt phẳng $(SAB),(SBC)$ bằng $60^0$.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Trong mặt phẳng $(P)$ cho tam giác $ABC$ vuông tại $C, AB=2a,\widehat{CAB}=60^0$, đoạn $SA=h$ và $SA$ vuông góc với $(P)$. Tìm $h$ sao cho góc giữa hai mặt phẳng $(SAB),(SBC)$ bằng $60^0$. Lời giải Kẻ $AH \bot SC, AK \bot SB ( H\in SC, K\in SB)$.Dễ dàng nhận thấy $\widehat{AKH}=\alpha$ là góc giữa hai mặt phẳng $(SAB),(SBC)$. Từ đó:$\alpha … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho tam giác $ABC$ vuông tại $C, AB=2a,\widehat{CAB}=60^0$, đoạn $SA=h$ và $SA$ vuông góc với $(P)$. Tìm $h$ sao cho góc giữa hai mặt phẳng $(SAB),(SBC)$ bằng $60^0$.

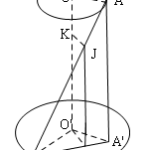
Đề bài: Trên hai mặt phẳng $(P)$ và $(P')$ song song nhau, ta vẽ tương ứng hai đường tròn $(O, R)$ và $(O', R')$, với $OO'\bot (P)$. Gọi $OA$ và $O'B$ theo thứ tự là hai bán kính của hai đường tròn trên sao cho $OA\bot OB$. Cho $OO'=h$.a) Vẽ đường vuông góc chung của $AB$ và $OO'$.b) Chứng minh đường vuông góc chung này qua một điểm cố định. Hãy tìm quỹ tích đầu mút di động của đoạn vuông góc chung này.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Trên hai mặt phẳng $(P)$ và $(P')$ song song nhau, ta vẽ tương ứng hai đường tròn $(O, R)$ và $(O', R')$, với $OO'\bot (P)$. Gọi $OA$ và $O'B$ theo thứ tự là hai bán kính của hai đường tròn trên sao cho $OA\bot OB$. Cho $OO'=h$.a) Vẽ đường vuông góc chung của $AB$ và $OO'$.b) Chứng minh đường vuông góc chung này qua một điểm cố định. … [Đọc thêm...] vềĐề bài: Trên hai mặt phẳng $(P)$ và $(P')$ song song nhau, ta vẽ tương ứng hai đường tròn $(O, R)$ và $(O', R')$, với $OO'\bot (P)$. Gọi $OA$ và $O'B$ theo thứ tự là hai bán kính của hai đường tròn trên sao cho $OA\bot OB$. Cho $OO'=h$.a) Vẽ đường vuông góc chung của $AB$ và $OO'$.b) Chứng minh đường vuông góc chung này qua một điểm cố định. Hãy tìm quỹ tích đầu mút di động của đoạn vuông góc chung này.

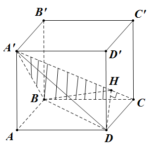
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$. Tìm số đo của góc tạo bởi hai mặt phẳng $(BA'C);(D'AC)$.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$. Tìm số đo của góc tạo bởi hai mặt phẳng $(BA'C);(D'AC)$. Lời giải Ta có: $(BA'C)\cap (DA'C)=A'C\Rightarrow A'DC$ là tam giác vuông tại $D$. Kẻ $DH \bot A'C.$ Hai tam giác vuông $A'DC; A'BC$ bằng nhau vì có chung cạnh huyền $A'C$ và $A'B=AD$, nên suy ra $BH\bot A'C$. Vậy $BHD$ chính là góc … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$. Tìm số đo của góc tạo bởi hai mặt phẳng $(BA'C);(D'AC)$.

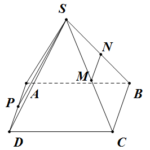
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$.

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$. Lời giải Giả sử $AC\cap MB=I$.Vì $MA=MD$ và do $AD//BC$,nên theo định lí Talet suy ra $AI=\frac{1}{2}IC$Do $AC^2=AD^2+DC^2=(a\sqrt{2})^2+a^2=3a^2$ … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$.

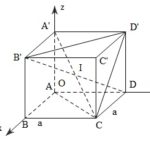
Đề bài: Cho hình lập phương $ABCD. A'B'C'D'$ biết bán kính hình cầu nội tiếp trong tứ diện $ACB'D'$ bằng $r$a) Tính diện tích toàn phần cửa tứ diện $ACB'D'$ theo $r$b) Tính thể tích khối lập phương $ABCD. A'B'C'D'$ theo $a$

Ngày 28/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho hình lập phương $ABCD. A'B'C'D'$ biết bán kính hình cầu nội tiếp trong tứ diện $ACB'D'$ bằng $r$a) Tính diện tích toàn phần cửa tứ diện $ACB'D'$ theo $r$b) Tính thể tích khối lập phương $ABCD. A'B'C'D'$ theo $a$ Lời giải a) Gọi $a$ là cạnh hình lập phương và $I$ là tâm hình cầu nội tiếp tứ … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD. A'B'C'D'$ biết bán kính hình cầu nội tiếp trong tứ diện $ACB'D'$ bằng $r$a) Tính diện tích toàn phần cửa tứ diện $ACB'D'$ theo $r$b) Tính thể tích khối lập phương $ABCD. A'B'C'D'$ theo $a$