Đề: Cho Elip $(E)$ có phương trình: $(E):\frac{x^2}{a^2}+\frac{y^2}{b^2}=1  $ với $0

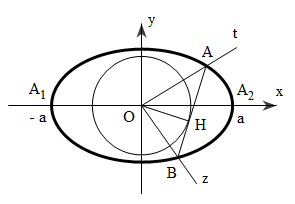
Đề bài: Cho Elip $(E)$ có phương trình: $(E):\frac{x^2}{a^2}+\frac{y^2}{b^2}=1  $ với $0

Lời giải

1. Tọa độ $A$ là nghiệm của hệ:
$\begin{cases}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1   \\ y=kx \end{cases} \Rightarrow  x_A^2=\frac{a^2b^2}{a^2k^2+b^2} $ và $y_A^2=\frac{k^2a^2b^2}{a^2k^2+b^2} $
Từ đó, suy ra:
$OA^2=x_A^2+y_A^2=\frac{a^2b^2}{a^2b^2+b^2}+\frac{k^2a^2b^2}{a^2k^2+b^2}=\frac{a^2b^2(1+k^2)}{a^2b^2+b^2}   $
$\Rightarrow  OA=ab \sqrt{\frac{1+k^2}{a^2k^2+b^2} }  $
2. Giả sử đường thẳng $(OA)$ có phương trình $y=kx\Rightarrow  OA=ab \sqrt{\frac{1+k^2}{a^2k^2+b^2} }  $
Vì $OA\bot OB\Rightarrow  (OB)$ có phương trình:
$y=-\frac{1}{k}x\Rightarrow  OB=ab\sqrt{\frac{1+\frac{1}{k^2} }{a^2.\frac{1}{k^2}+b^2} }  =ab\sqrt{\frac{1+k^2}{a^2+b^2k^2} } $
a. Ta có: $\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{a^2k^2+b^2}{a^2b^2(1+k^2)}+\frac{a^2+b^2k^2}{a^2b^2(1+k^2)} =\frac{a^2+b^2}{a^2b^2}    $ không đổi
Gọi $H$ là hình chiếu vuông góc của $O$ lên $AB$, khi đó: $\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{a^2+b^2}{a^2b^2}    \Rightarrow  OH=\frac{ab}{\sqrt{a^2+b^2} } $
Vậy $AB$ luôn tiếp xúc với đường tròn $(C)$ tâm $O$ bán kính $R=OH$ có:
$(C):x^2+y^2=\frac{a^2b^2}{a^2+b^2} $
b. Ta có:
$S_{\Delta OAB}=\frac{1}{2}OA.OB=\frac{1}{2}ab\sqrt{\frac{1+k^2}{a^2k^2+b^2} }ab\sqrt{\frac{1+k^2}{a^2+b^2k^2} }=\frac{a^2b^2(1+k^2)}{2\sqrt{(a^2k^2+b^2)(a^2+b^2k^2)} }       (1)$
$-  \Delta OAB$ có diện tích nhỏ nhất, ta có:
$\sqrt{(a^2k^2+b^2)(a^2+b^2k^2)}\leq  \frac{(a^2k^2+b^2)+(a^2+b^2k^2)}{2}=\frac{(a^2+b^2)(1+k^2)}{2}  $
$\Rightarrow  \frac{1+k^2}{\sqrt{(a^2k^2)(a^2+b^2k^2)} } \geq  \frac{2}{a^2+b^2}        (2)$
Thay $(2)$ vào $(1)$, ta được: $S_{\Delta OAB}\geq  \frac{ab}{a^2+b^2} \Rightarrow  S_{Min}=\frac{ab}{a^2+b^2} $ đạt được khi: $a^2k^2+b^2=a^2+b^2k^2\Leftrightarrow  k= \pm 1$
$-  \Delta OAB$ có diện tích lớn nhất (Bạn đọc tự giải)