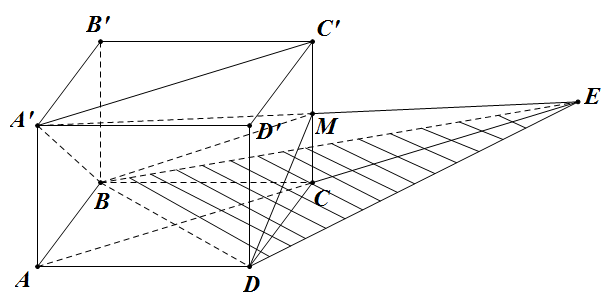
Đề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ đáy là hình vuông cạnh bằng $a$, chiều cao $AA'=b$. Gọi $M$ là trung điểm của cạnh $CC'$. Tính thể tích tứ diện $BDA'M$.

Lời giải

 Trong $(ACC’A’): A’M \cap AC=E.$ Gọi $O$ là tâm của đáy $ABCD$ vì $M$ là trung điểm của $CC’$ , nên ta có  $ CE=AC=a\sqrt{2}$
Ta có:
    $V_{A’BDM}=V_{A’BDE}-V_{M.BDE}=\frac{1}{3}S_{BDE}.AA’-\frac{1}{3}S_{BDE}.MC$
                     $=\frac{1}{3}S_{BDE}(AA’-MC)$
                     $=\frac{1}{3}.\frac{1}{2}BD.EO(b-\frac{b}{2})=\frac{1}{6}.a\sqrt{2}.\frac{3}{2}.a\sqrt{2}.\frac{b}{2}=\frac{a^2b}{4}$ (đvtt).