Cho hàm số $y = f(x) = \dfrac{ax^2 + bx + c}{dx + e}$ với đồ thị $(\mathscr{C})$ và bảng biến thiên bên dưới

Bài toán gốc

Cho hàm số $y = f(x) = \dfrac{ax^2 + bx + c}{dx + e}$ với đồ thị $(\mathscr{C})$ và bảng biến thiên bên dưới

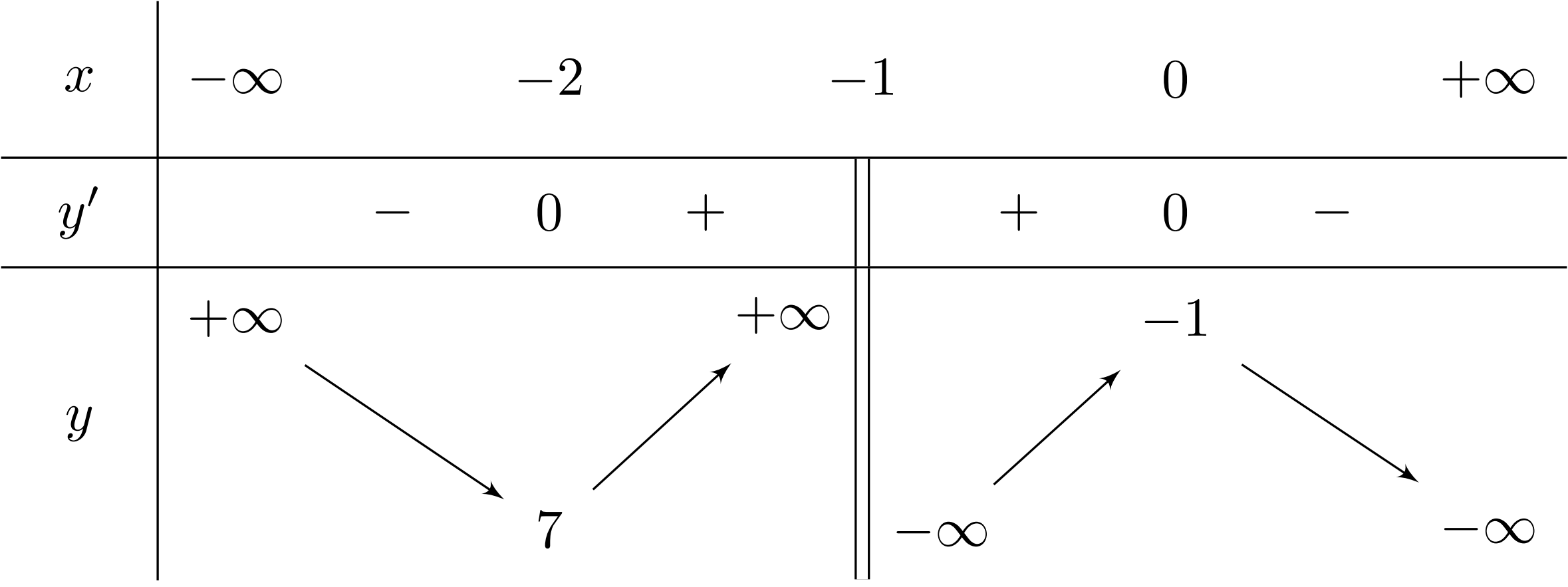
Khi đó đồ thị hàm số có đường tiệm cận đứng là

A. $x = -1$.

B. $x = 0$.

C. $y = -1$.

D. $x = -2$.

Lời giải: Dựa vào bảng biến thiên ta có đường tiệm cận đứng của đồ thị $(\mathscr{C})$ là $x = -1.$

Phân tích và Phương pháp giải

Đây là dạng bài toán xác định đường tiệm cận đứng (TCD) của hàm số dựa vào bảng biến thiên. Đường tiệm cận đứng của đồ thị hàm số $y=f(x)$ là đường thẳng $x = x_0$ nếu tại đó $\lim_{x \to x_0^+} f(x) = \pm \infty$ hoặc $\lim_{x \to x_0^-} f(x) = \pm \infty$. Trong bảng biến thiên, TCD ứng với giá trị $x$ làm cho hàm số không xác định (hai gạch song song) và giá trị của $y$ tiến tới vô cực.

Bài toán tương tự

Cho hàm số $y = f(x)$ có bảng biến thiên được mô tả như sau: trên khoảng xác định, khi $x$ tiến tới $2$ từ bên trái ($x \to 2^-$) thì $y \to -\infty$, và khi $x$ tiến tới $2$ từ bên phải ($x \to 2^+$) thì $y \to +\infty$. Khi đó, đồ thị hàm số có đường tiệm cận đứng là gì?A. $x = 2$.B. $y = 2$.C. $x = -2$.D. $y = -2$.Đáp án đúng: A. Lời giải: Dựa vào thông tin giới hạn, ta thấy khi $x$ tiến tới $2$ thì giá trị hàm số tiến tới vô cực. Theo định nghĩa, đường thẳng $x = 2$ chính là đường tiệm cận đứng của đồ thị hàm số.