Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận ngang của đồ thị hàm số là

Bài toán gốc

Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận ngang của đồ thị hàm số là

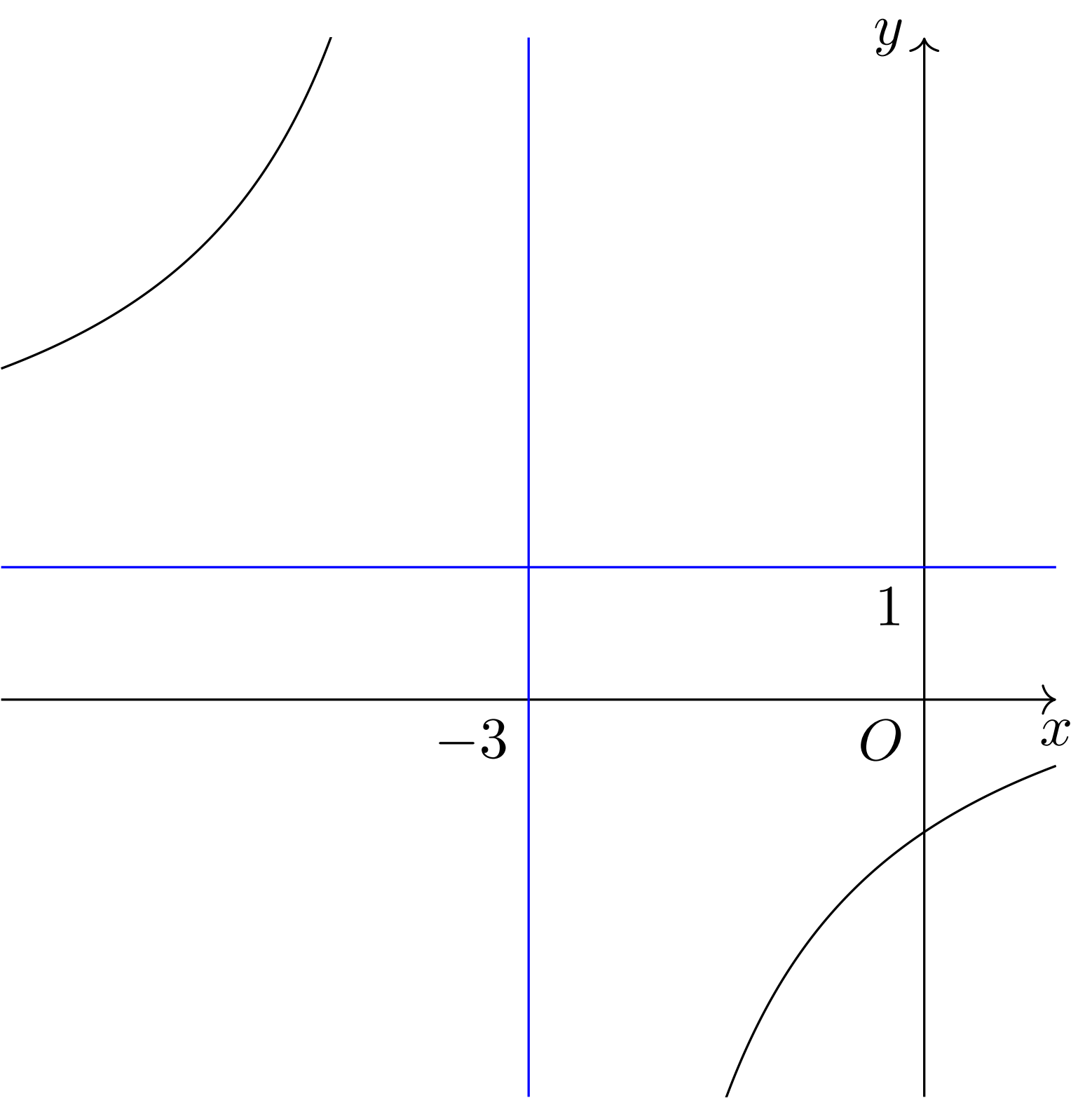
A. $y = 1$.

B. $y = -1$.

C. $x = -1$.

D. $x = 1$.

Lời giải: Dựa vào đồ thị hàm số ta thấy tiệm cận ngang của đồ thị hàm số là $y = 1$

Phân tích và Phương pháp giải

Đây là dạng bài tập nhận biết tiệm cận ngang (TCN) của đồ thị hàm số thông qua đồ thị. Phương pháp giải là quan sát hành vi của đồ thị khi $x \to +\infty$ và $x \to -\infty$. Nếu đồ thị tiến sát đến đường thẳng nằm ngang $y=L$, thì $y=L$ chính là TCN của đồ thị hàm số.

Bài toán tương tự

Cho hàm số $y = g(x)$ có đồ thị. Khi quan sát đồ thị, ta thấy rằng khi $x$ tiến tới dương vô cùng $(x \to +\infty)$, đồ thị hàm số tiến sát đến đường thẳng nằm ngang $y = -2$. Tiệm cận ngang của đồ thị hàm số $y = g(x)$ là:\nA. $y = 2$.\nB. $x = -2$.\nC. $y = -2$.\nD. $x = 2$.\n\nĐáp án đúng: C.\nLời giải ngắn gọn: Tiệm cận ngang (TCN) là đường thẳng $y=L$ nếu $\lim_{x\to \pm\infty} g(x) = L$. Dựa vào mô tả hành vi của đồ thị, khi $x \to +\infty$, đồ thị tiến sát đường thẳng $y = -2$. Do đó, tiệm cận ngang của đồ thị là $y = -2$.