Bài toán gốc
Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận đứng của đồ thị hàm số là
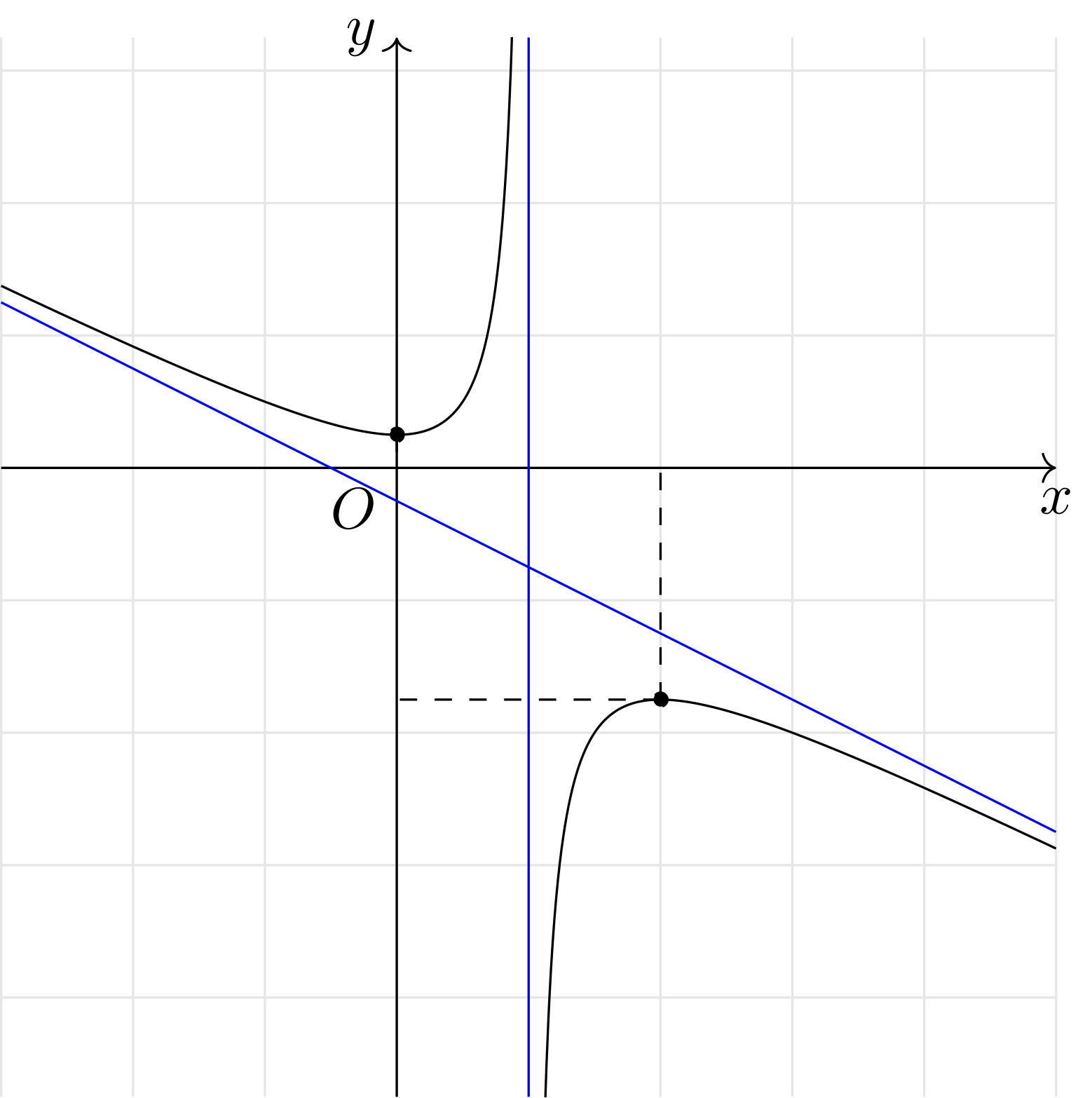
A. $y = – \dfrac{x}{2} – \dfrac{1}{4}$.
B. $x = -1$.
C. $x = – \dfrac{3}{4}$.
D. $y = -4x + 2$.
Lời giải: Dựa vào đồ thị hàm số ta thấy tiệm cận đứng của đồ thị hàm số là $y = – \dfrac{3}{4}$
Phân tích và Phương pháp giải
Đây là dạng bài toán nhận dạng các đường tiệm cận của đồ thị hàm số thông qua việc quan sát hình vẽ. Tiệm cận đứng (TCD) là đường thẳng đứng có phương trình $x=a$ mà tại đó hàm số không xác định và $\lim_{x \to a^{\pm}} f(x) = \pm \infty$. Trong bài toán gốc, mặc dù lời giải đưa ra có vẻ bị nhầm lẫn giữa $x$ và $y$ (TCD phải có dạng $x=a$), phương pháp giải vẫn là xác định đường thẳng đứng mà đồ thị tiến sát.
Bài toán tương tự
Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới (Giả sử đồ thị là hàm phân thức có hai nhánh). Quan sát đồ thị, nếu đường cong tiến sát vô hạn đến đường thẳng $x = 3$. Khi đó tiệm cận đứng của đồ thị hàm số là:
A. $y = 3$.
B. $x = 3$.
C. $x = 1$.
D. $y = -2$.
Đáp án đúng: B. $x = 3$.
Lời giải ngắn gọn: Dựa vào đồ thị hàm số, ta thấy rằng khi $x$ tiến dần về $3$ (cả bên trái và bên phải), giá trị của hàm số $f(x)$ tiến tới vô cùng (dương vô cùng hoặc âm vô cùng). Do đó, đường thẳng $x = 3$ là tiệm cận đứng của đồ thị hàm số.
