Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận đứng của đồ thị hàm số là

Bài toán gốc

Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận đứng của đồ thị hàm số là

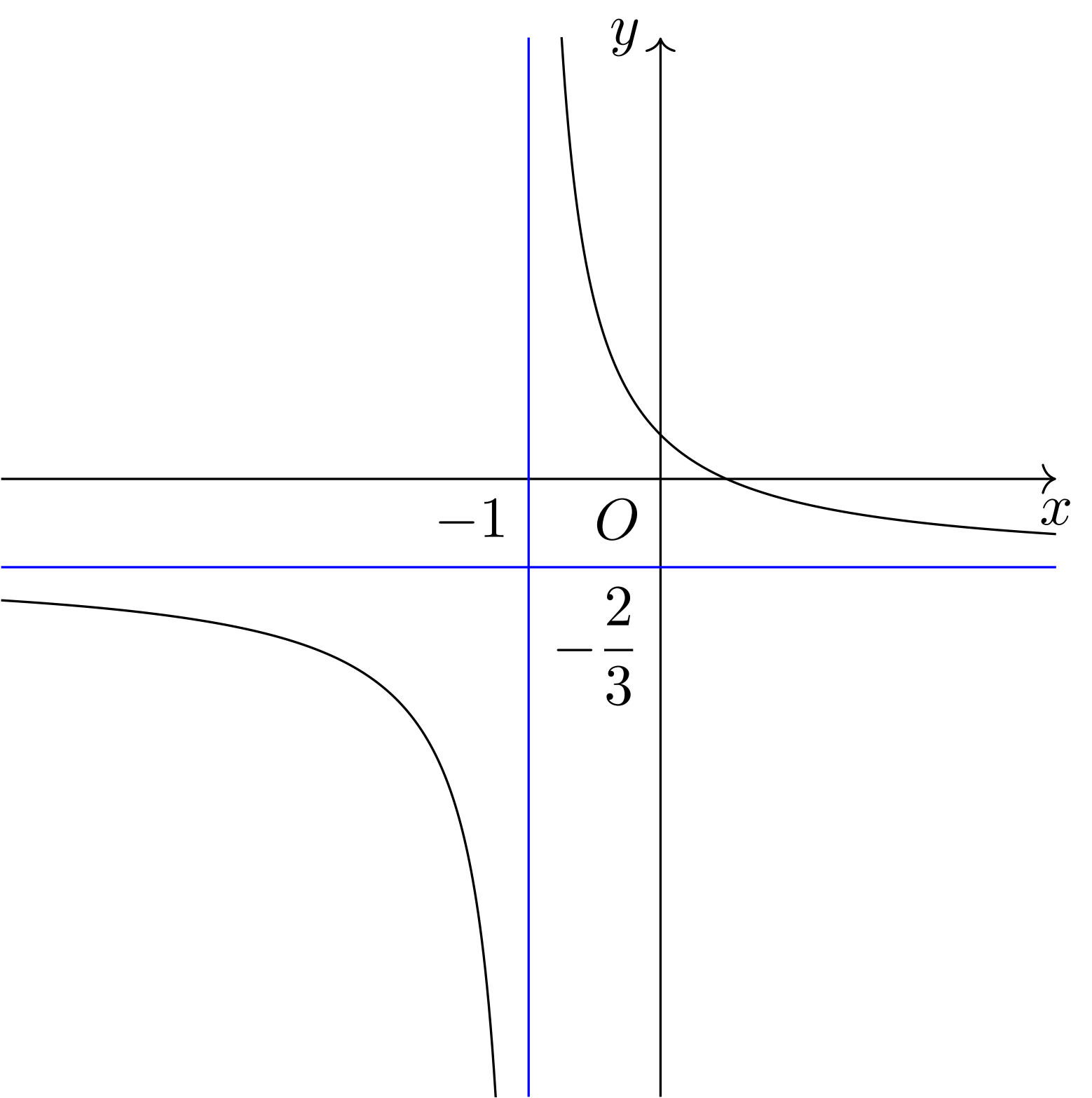
A. $x = -1$.

B. $y = \dfrac{2}{3}$.

C. $x = \dfrac{2}{3}$.

D. $y = -1$.

Lời giải: Dựa vào đồ thị hàm số ta thấy tiệm cận đứng của đồ thị hàm số là $x = -1$

Phân tích và Phương pháp giải

Dạng bài toán: Nhận dạng tiệm cận của hàm số dựa vào đồ thị. Phương pháp: Tiệm cận đứng $x=a$ là giá trị mà tại đó giới hạn của hàm số tiến đến vô cực ($\lim_{x \to a^\pm} f(x) = \pm \infty$). Tiệm cận ngang $y=b$ là giá trị mà tại đó giới hạn của hàm số khi $x$ tiến đến vô cực là một hằng số ($\lim_{x \to \pm \infty} f(x) = b$). Bài toán gốc yêu cầu xác định tiệm cận đứng bằng cách quan sát đường thẳng đứng mà đồ thị tiến sát.

Bài toán tương tự

Cho hàm số $y = h(x)$ có đồ thị. Quan sát đồ thị, ta thấy khi $x \to +\infty$ và $x \to -\infty$, đồ thị hàm số tiến dần về đường thẳng $y = 2$. Khi đó, tiệm cận ngang của đồ thị hàm số là: A. $x = 2$. B. $y = 2$. C. $x = -2$. D. $y = 0$. Đáp án đúng: B. Lời giải ngắn gọn: Tiệm cận ngang của đồ thị hàm số là đường thẳng $y=b$ mà đồ thị tiến sát khi $x \to \pm \infty$. Dựa vào giả thiết, khi $x \to \pm \infty$, đồ thị tiến về $y = 2$. Vậy $y = 2$ là tiệm cận ngang.