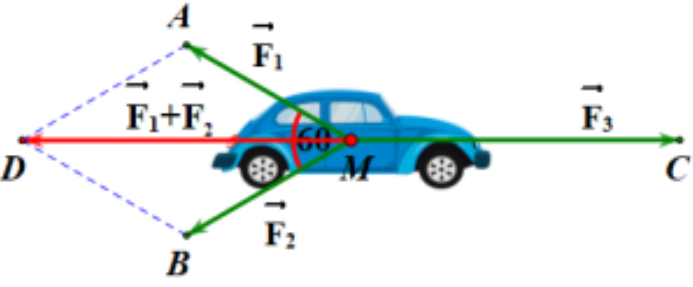
Cho ba lực $\overrightarrow{F_1}=\overrightarrow{M A}, \overrightarrow{F_2}=\overrightarrow{M B}, \overrightarrow{F_3}=\overrightarrow{M C}$ cùng tác động vào một ô tô tại điểm $M$ và ô tô đứng yên. Cho biết cường độ hai lực $\vec{F}_1, \bar{F}_2$ đều bằng 25 N và góc $\widehat{A M B}=60^{\circ}$. Khi đó cường độ lực $\vec{F}_3$ là (Kết quả làm tròn đên hàng phần mười)
Lời giải
Đáp số: 43,3
– Ta có: $\vec{F}_1+\vec{F}_2=\overrightarrow{M A}+\overrightarrow{M B}=\overrightarrow{M D}$ (Vói $D$ là điểm sao cho $AMBD$ là hình bình hành)
– Ta có:
$\begin{array}{l} MA=|\overrightarrow{MA}|=\left| {{{\vec{F}}}_{1}} \right|=25\text{N} \\
MB=|\overrightarrow{MB}|=\left| {{{\vec{F}}}_{2}} \right|=25N \\ \end{array}$
– Do $\widehat{AMB}=60{}^\circ$ nên $\triangle M A B$ là tam giác đều. Khi đó: $M D=2 \cdot \dfrac{25 \sqrt{3}}{2}=25 \sqrt{3}$
– Do ô tô đứng yên nên $\vec{F}_1+\vec{F}_2+\vec{F}_3=\overrightarrow{0}$
Suy ra: $\vec{F}_3=-\left(\vec{F}_1+\vec{F}_2\right) \Rightarrow\left|\vec{F}_3\right|=\left|-\left(\vec{F}_1+\vec{F}_2\right)\right|=|\overrightarrow{D M}|=M D=25 \sqrt{3}(N)$
Vậy cường độ của $\overrightarrow{F_3}$ là $25 \sqrt{3} \approx 43,3(N)$.
