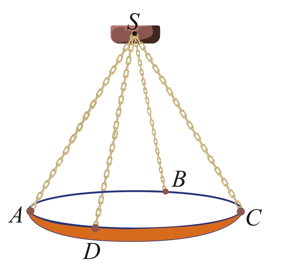
Một chiếc đèn chùm treo có khối lượng $m=8kg$ được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích $SA,SB,SC,SD$ sao cho $S.ABCD$ là hình chóp tứ giác đều có $\widehat{ASC}={{60}^{{}^\circ }}$ (Hình).
Biết $\vec{P}=m\vec{g}$ trong đó $\vec{g}$ là vectơ gia tốc rơi tự do có độ lớn $9,8m/{{s}^{2}}$, $\vec{P}$ là trọng lực tác động vật có đơn bị là $N$, $m$ là khối lượng của vật có đơn vị $kg$. Tính độ lớn của lực căng cho mỗi sợi xích (tính chính xác đến hàng phần mười).
Lời giải
Trả lời: 17
Ta có $P=8.9,8=78,4N$
Vì $S.ABCD$ là hình chóp tứ giác đều nên $SA=SB=SC=SD$
Mà $\widehat{ASC}={{60}^{{}^\circ }}={>}$ Tam giác $SAC$ đều
Gọi $O$ là trung điểm $AC$.
Ta có: Hợp lực của 4 sợi xích là $\vec{F}=\overrightarrow{SA}+\overrightarrow{SC}+\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}+2\overrightarrow{SO}=4\overrightarrow{SO}$
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay $4\overrightarrow{SO}=\vec{P}$ hay $4SO=P\Leftrightarrow SO=19,6$
Xét tam giác đều $SAC:SA=\dfrac{\sqrt{3}}{2}SO=\dfrac{19,6.\sqrt{3}}{2}\approx 17$
Vậy độ lớn của lực căng cho mỗi sợi xích là $17N.$
