Một chiếc cân đòn tay đang cân một vật có khối lượng $m=3kg$ được thiết kế với đĩa cân được giữ bởi bốn đoạn xích $SA,SB,SC,SD$ sao cho $S.ABCD$ là hình chóp tứ giác đều có $\widehat{ASC}=90{}^\circ$. Biết độ lớn của lực căng mỗi sợi xích có dạng $\dfrac{a\sqrt{2}}{4}\left( N \right)$. Biết trọng lượng của vật nặng được tính theo công thức $P=mg$, lấy $g=10\text{m/}{{\text{s}}^{\text{2}}}$. Khi đó giá trị của $a$ bằng bao nhiêurx8|?
Lời giải
Đáp án: $30$.
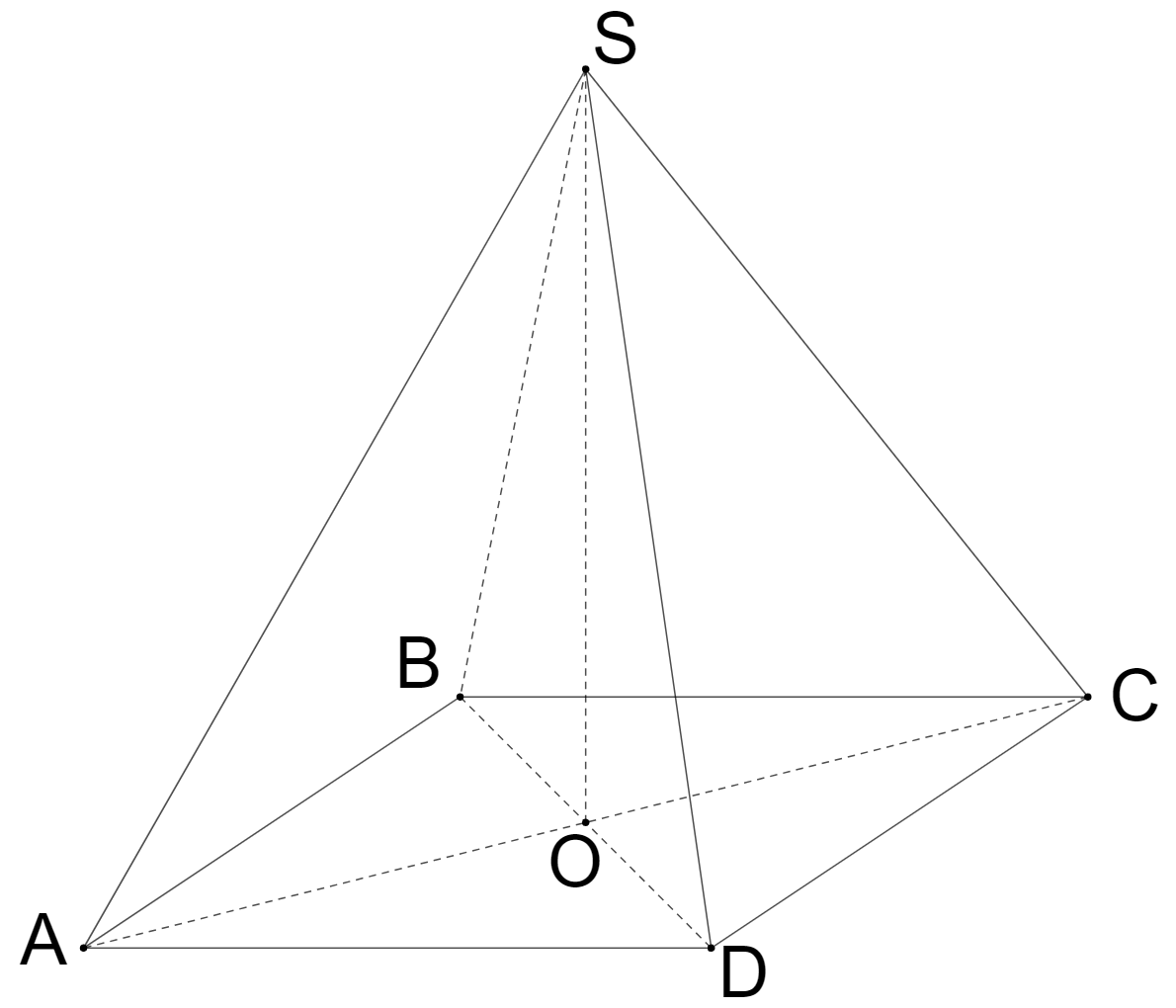
Ta mô hình hóa chiếc cân bởi hình chóp đều $S.ABCD$ với $\left| \overrightarrow{SA} \right|=\left| \overrightarrow{SB} \right|=\left| \overrightarrow{SC} \right|=\left| \overrightarrow{SD} \right|=\dfrac{a\sqrt{2}}{4}$
Ta có: $\Delta SAC$ vuông cân tại $S$ nên235| $AC=\dfrac{a\sqrt{2}}{4}.\sqrt{2}=\dfrac{a}{2}$.
Suy ra $BD=AC=\dfrac{a}{2}$. Từ đó suy ra $AB=AD=CD=BC=\dfrac{a\sqrt{2}}{4}$.
Vậy các mặt bên đều là tam giác đều.
Ta có: $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=4\overrightarrow{SO}$ mà $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{P}$
Suy ra $4\overrightarrow{SO}=\overrightarrow{P}\Leftrightarrow \overrightarrow{SO}=\dfrac{1}{4}\overrightarrow{P}$ nên ta có $SO=\dfrac{1}{4}P=\dfrac{1}{4}mg=\dfrac{1}{4}3.10=\dfrac{15}{2}$.
Do $\Delta SAC$ vuông cân tại $S$ nên $SO=\dfrac{1}{2}AC$ $\Leftrightarrow \dfrac{15}{2}=\dfrac{1}{2}.\dfrac{a}{2}\Leftrightarrow a=30$.
Vậy $a=30$.
