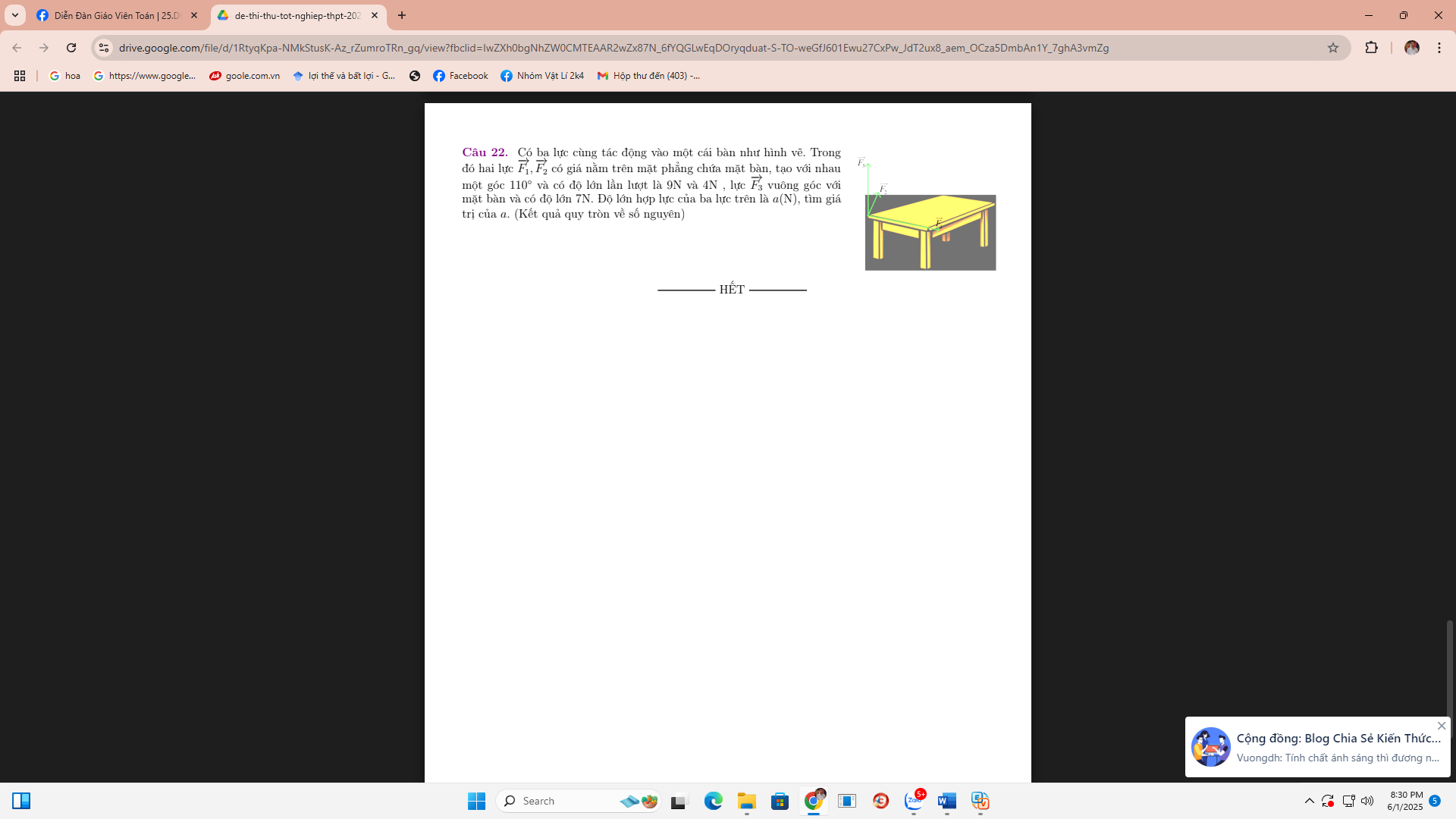
Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực $\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}}$ có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc ${{110}^{0}}$ và có độ lớn lần lượt là $9N$ và $4N$, lực $\overrightarrow{{{F}_{3}}}$ vuông góc với mặt bàn và có độ lớn $7N$. Độ lớn hợp lực của ba lực trên là $a\left( N \right)$, tìm giá trị của $a$. (kết quả quy tròn về số nguyên).
Lời giải
Đáp án: 11.
Ta có
$\begin{array}{l} \overrightarrow{{{F}_{12}}}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}\Rightarrow \left| \overrightarrow{{{F}_{12}}} \right|=\left| \overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}} \right|=\sqrt{{{\left| \overrightarrow{{{F}_{1}}} \right|}^{2}}+{{\left| \overrightarrow{{{F}_{2}}} \right|}^{2}}+2\left| \overrightarrow{{{F}_{1}}} \right|.\left| \overrightarrow{{{F}_{2}}} \right|.cos\left( \overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}} \right)} \\ =\sqrt{{{9}^{2}}+{{4}^{2}}+2.9.4.\cos {{110}^{0}}}\approx 8,5 \\ \end{array}$.
$\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=\overrightarrow{{{F}_{12}}}+\overrightarrow{{{F}_{3}}}\Rightarrow \left| \overrightarrow{F} \right|=\left| \overrightarrow{{{F}_{12}}}+\overrightarrow{{{F}_{3}}} \right|=\sqrt{{{\left| \overrightarrow{{{F}_{12}}} \right|}^{2}}+{{\left| \overrightarrow{{{F}_{3}}} \right|}^{2}}}=\sqrt{{{\left( 8,5 \right)}^{2}}+{{7}^{2}}}\approx 11N$.
Vậy $a$ sấp xỉ bằng $11$.
