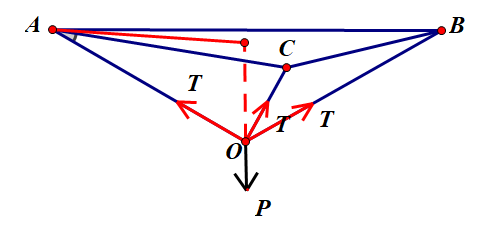
Người ta treo một chiếc đèn trang trí có trọng lượng 200N lên trần nhà bằng ba sợi dây không giãn, bằng nhau tại ba điểm A,B,C tạo thành tam giác đều. Mỗi sợi dây tạo với mặt phẳng trần nhà một góc 30 đến được giữ ở trạng thái cân bằng (tham khảo hình vẽ). Hãy tính lực căng trong mỗi sợi dây (kết quả làm tròn đến hàng đơn vị).
Lời giải
 Đáp án: $133$
Đáp án: $133$
Lực căng của mỗi sợi dây là $\dfrac{400}{3} N$.
Khi cân bằng:
$\vec{T}_A+\vec{T}_B+\vec{T}_C+\vec{P}=0$
Các lực $\vec{T}_A, \vec{T}_B, \vec{T}_C$ có độ lớn bằng nhau đều là $T(N)$, hợp lực theo phương song song với mặt trần bằng 0.
Theo phương thẳng đứng:
${{T}_{A}}\sin \alpha +{{T}_{B}}\sin \alpha +{{T}_{C}}\sin \alpha =P\Leftrightarrow 3T\sin \alpha =P\Leftrightarrow T=\dfrac{P}{3\sin \alpha }=\dfrac{200}{3\sin {{30}^{{}^\circ }}}=\dfrac{400}{3}\approx 133(N)$
