Có ba lực cùng tác động vào một vật, Hai trong ba lực này hợp với nhau một góc ${{100}^{\circ }}$ và có độ lớn lần lượt là $25$ N và $12$ N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn $4$ N. Tính độ lớn của hợp lực của ba lực trên (làm tròn đến hàng phần chục).
Lời giải
Đáp án: 26,1.
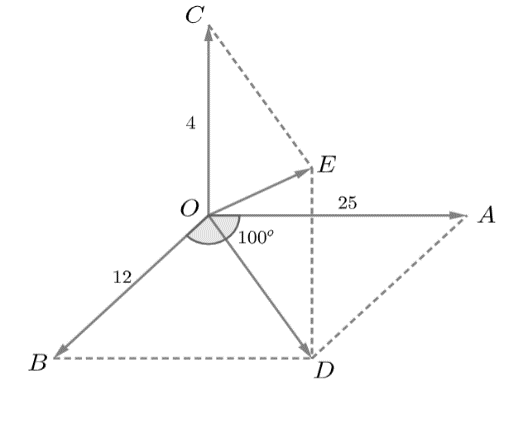
Gọi $\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}},\overrightarrow{{{F}_{3}}}$ là ba lực tác động vào vật tại điểm $\text{O}$ lần lượt có độ lớn $25\text{N},12\text{N},4\text{N}$.
Vẽ $\overrightarrow{OA}=\overrightarrow{{{F}_{1}}},\overrightarrow{OB}=\overrightarrow{{{F}_{2}}},\overrightarrow{OC}=\overrightarrow{{{F}_{3}}}$, dựng hình bình hành $OADB$ và $ODEC$.
Khi đó hợp lực tác động vào vật là: $\overrightarrow{F}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{OE}$.
Áp dụng định lý cô sin trong tam giác $OBD,$ ta có:
$O{{D}^{2}}=O{{B}^{2}}+B{{D}^{2}}-2OB.BD\cos\widehat{OBD}={{12}^{2}}+{{25}^{2}}-2.12.25.\cos {{80}^{\circ }}=769-600.\cos 80{}^\circ$
Vì $OC\bot \left( OADB \right)$ nên $OC\bot OD$, suy ra $ODEC$ là hình chữ nhật. Do đó tam giác $ODE$ vuông tại $D$. Ta có $OE=\sqrt{O{{D}^{2}}+E{{D}^{2}}}\approx 26,1$
