Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc ${120^{\circ}}$ và có độ lớn lần lượt là 10 N và 8 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 6 N. Tính độ lớn của hợp lực của ba lực trên. (Làm tròn kết quả đến hàng đơn vị)
Lời giải
Đáp số: 11
Gọi ${\vec{F}_1, \vec{F}_2, \vec{F}_3}$ lần lượt là ba lực tác động vào một vật đặt tại điểm ${O}$ như Hình.
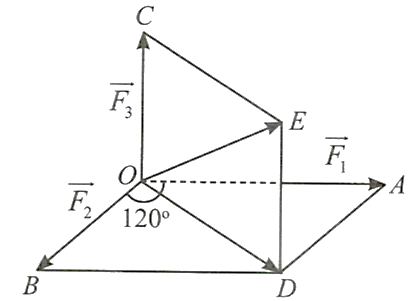
Ta có ${\vec{F}_1=\overrightarrow{O A}, \vec{F}_2=\overrightarrow{O B}, \overrightarrow{F_3}=\overrightarrow{O C}}$.
Độ lớn các lực: ${F_1=O A=10 {N}, F_2=O B=8 {N}}$, ${F_3=O C=6 {N}}$.
Dựng hình bình hành ${O A D B}$. Theo quy tắc hình bình hành, ta có ${\overrightarrow{O D}=\overrightarrow{O A}+\overrightarrow{O B}}$.
Suy ra ${\overrightarrow{O D}^2=(\overrightarrow{O A}+\overrightarrow{O B})^2=\overrightarrow{O A}^2+\overrightarrow{O B}^2+2 \overrightarrow{O A} \cdot \overrightarrow{O B}}$.
Mà ${\overrightarrow{O A} \cdot \overrightarrow{O B}=O A \cdot O B \cdot \cos (\overrightarrow{O A}, \overrightarrow{O B})}$, suy ra ${O D^2=O A^2+O B^2+2 \cdot O A \cdot O B \cdot \cos 120^{\circ}}$.
Dựng hình bình hành ${O D E C}$.
Tổng lực tác động vào vật là ${\vec{F}=\overrightarrow{O E}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}}$.
Độ lớn của hợp lực tác động vào vật là ${F=O E}$.
Vì ${O C \perp(O A D B)}$ nên ${O C \perp O D}$, suy ra ${O D E C}$ là hình chữ nhật.
Do đó tam giác ${O D E}$ vuông tại ${D}$.
Khi đó, ${O E^2=O C^2+O D^2=O C^2+O A^2+O B^2+2 \cdot O A \cdot O B \cdot \cos 120^{\circ}}$.
Suy ra ${O E=\sqrt{O C^2+O A^2+O B^2+2 \cdot O A \cdot O B \cdot \cos 120^{\circ}}}$
$=\sqrt{{{6}^{2}}+{{10}^{2}}+{{8}^{2}}+2\cdot 10\cdot 8\cdot \cos {{120}^{{}^\circ }}}\approx 11$
Do đó $F=OE\approx 11N$.
