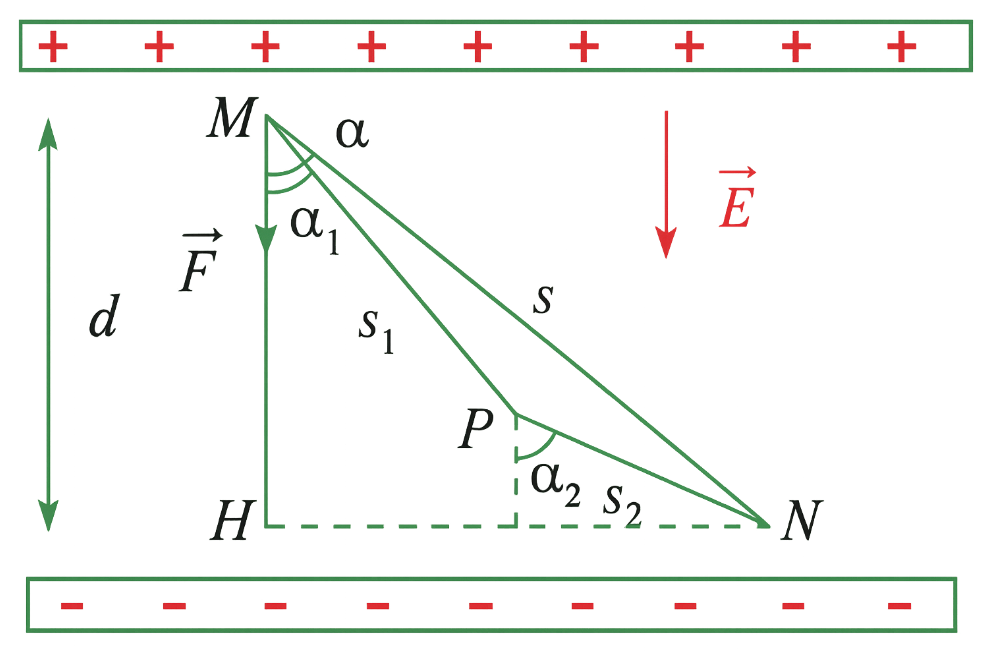
Một lực tĩnh điện ${\vec{F}}$ tác động lên điện tích điểm ${M}$ trong điện trường đều làm cho ${M}$ dịch chuyển theo đường gấp khúc ${M N P}$ (Hình). Biết ${q=2 \cdot 10^{-12} {C}}$, vectơ điện trường có độ lớn ${E=1,8 \cdot 10^5 {N} / {C}}$ và ${d=M H=5 {mm}}$. Tính được công $A$ sinh bởi lực tĩnh điện ${\vec{F}}$ bằng $a{{.10}^{b}}(J),\left( a\in \mathbb{R};b\in \mathbb{Z} \right)$. Tìm $a+b$
Lời giải
Trả lời: -7,2
Đổi: ${5 {mm}=0,005 {m}}$
Gọi $K$ là điểm thuộc $MH$ sao cho ${P K \perp M H}$, $L$ là điểm thuộc ${{HN}}$ sao cho ${P L \perp H N}$
${\begin{array}{l} A_{M N P}=A_{M P}+A_{P N}=F_d \cdot M P \cos \alpha_1+F_d \cdot P N \cos \alpha_2 \\ \Leftrightarrow A_{M N P}=q E \cdot \dfrac{M K}{\cos \alpha_1} \cdot \cos \alpha_1+q E \cdot \dfrac{P L}{\cos \alpha_2} \cdot \cos \alpha_2 \\ \Leftrightarrow A_{M N P}=q E(M K+P L)=q E(M K+K H)=q E \cdot M H=2 \cdot 10^{-12} \cdot 1,8 \cdot 10^5 \cdot 0,005=1,8 \cdot 10^{-9} J \end{array}}$
