Ta đã biết trọng tâm của tứ diện ${A B C D}$ là một điểm $I$ thoả mãn ${\overrightarrow{A I}=3 \overrightarrow{I G}}$, ở đó ${G}$ là trọng tâm của tam giác ${B C D}$. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó (đơn vị cm), biết rằng chiều cao của khối rubik là ${8 {cm}}$.
Lời giải
Trả lời: 2
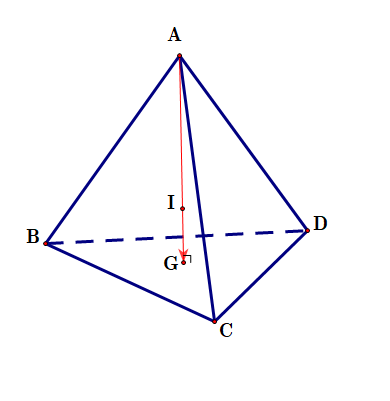
Đặt tên khối rubik là tứ diện đều ${A B C D}$ có ${G}$ là trọng tâm tam giác ${B C D}$, $I$ là trọng tâm tứ diện ${A B C D}$. Do đó, ${\overrightarrow{A I}=3 \overrightarrow{I G} \Rightarrow I G=\dfrac{1}{4} A G}$
Vì chiều cao của rubik bằng ${8 {cm}}$ nên ${A G=8 {cm} \Rightarrow I G=\dfrac{1}{4} .8=2({cm})}$
Vậy khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó bằng ${2 {cm}}$.
