Bài toán gốc
Cho hàm số $y=\dfrac{ax+b}{cx+d},(ad-bc\neq 0)$. Có đồ thị như hình dưới đây:
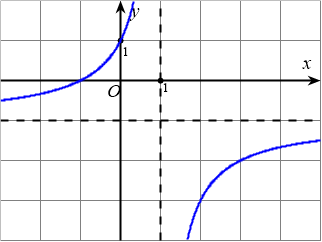
Chọn phát biểu sai?
A. Tâm đối xứng của đồ thị là $I\left(1;-1\right)$.
B. Tiệm cận đứng có phương trình $x=1$.
C. Tiệm cận ngang có phương trình $y=-1$.
D. Hàm số nghịch biến trên từng khoảng xác định.
Phân tích và Phương pháp giải
Bài toán yêu cầu xác định phát biểu sai về đồ thị hàm phân thức bậc nhất trên bậc nhất $y=\dfrac{ax+b}{cx+d}$. Phương pháp giải dựa trên việc xác định các yếu tố cơ bản của đồ thị: Tiệm cận đứng (nghiệm mẫu số), Tiệm cận ngang (tỷ lệ hệ số $a/c$), Tâm đối xứng (giao điểm hai tiệm cận), và kiểm tra tính đơn điệu (dấu của đạo hàm $y’ = \dfrac{ad-bc}{(cx+d)^2}$). Trong bài toán gốc, A, B, C mô tả các yếu tố hình học của đồ thị dựa trên tiệm cận $x=1$ và $y=-1$. Phát biểu sai thường liên quan đến tính đơn điệu (D), tức là tính đơn điệu được nêu ra bị ngược so với đồ thị thực tế (nếu đồ thị hiển thị đồng biến thì đáp án D là nghịch biến, hoặc ngược lại).
Bài toán tương tự
Cho hàm số $y=\dfrac{2x-1}{x+3}$. Chọn phát biểu SAI trong các phát biểu sau?
Đáp án đúng: D
Lời giải ngắn gọn: Hàm số đã cho có $a=2, b=-1, c=1, d=3$. Ta tính đạo hàm: $y’ = \dfrac{ad-bc}{(x+3)^2} = \dfrac{2(3) – (-1)(1)}{(x+3)^2} = \dfrac{6+1}{(x+3)^2} = \dfrac{7}{(x+3)^2}$. Vì $y’ > 0$ với mọi $x \neq -3$, hàm số đồng biến trên từng khoảng xác định. Phát biểu D (Hàm số nghịch biến) là sai. Các phát biểu A, B, C đều đúng (V.A $x=-3$, H.A $y=2$, Tâm đối xứng $I(-3; 2)$).
