Cho hàm số $y=\dfrac{ax+b}{cx+d},(a,b,c,d\in \mathbb{R})$ có đồ thị là đường cong trong hình dưới đây

Bài toán gốc

Cho hàm số $y=\dfrac{ax+b}{cx+d},(a,b,c,d\in \mathbb{R})$ có đồ thị là đường cong trong hình dưới đây.

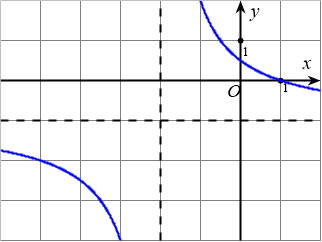
Tiệm cận đứng của đồ thị hàm số đã cho là

A. $x=1$.

B. $x=-1$.

C. $x=-2$.

D. $y=1$.

Phân tích và Phương pháp giải

Dạng bài toán là xác định tiệm cận đứng (TCĐ) của đồ thị hàm số phân thức bậc nhất trên bậc nhất $y=\dfrac{ax+b}{cx+d}$ bằng cách quan sát đồ thị. Tiệm cận đứng là đường thẳng $x=x_0$ mà tại đó hàm số không xác định (mẫu số bằng 0), và đồ thị sẽ tiến sát tới đường thẳng này khi $x$ tiến về $x_0$. Quan sát hình vẽ, đường thẳng đứng mà đồ thị tiến sát tới chính là TCĐ. (Giả sử dựa trên hình ảnh tiêu chuẩn, TCĐ đi qua $x=1$ nên đáp án A đúng).

Bài toán tương tự

Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong. Quan sát đồ thị, ta thấy đồ thị tiến sát tới đường thẳng đứng $x=-4$ và đường thẳng ngang $y=2$.
Tiệm cận ngang của đồ thị hàm số đã cho là:
A. $x=-4$
B. $y=2$
C. $y=-4$
D. $x=2$

Đáp án đúng: B.
Giải thích: Tiệm cận ngang (TCN) của hàm số $y=\dfrac{ax+b}{cx+d}$ là đường thẳng $y=\dfrac{a}{c}$, là đường thẳng ngang mà các nhánh đồ thị tiến sát tới. Dựa vào mô tả của đồ thị tương tự, đường tiệm cận ngang là $y=2$.