Bài toán gốc
Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Khi đó tiệm cận xiên của đồ thị hàm số là
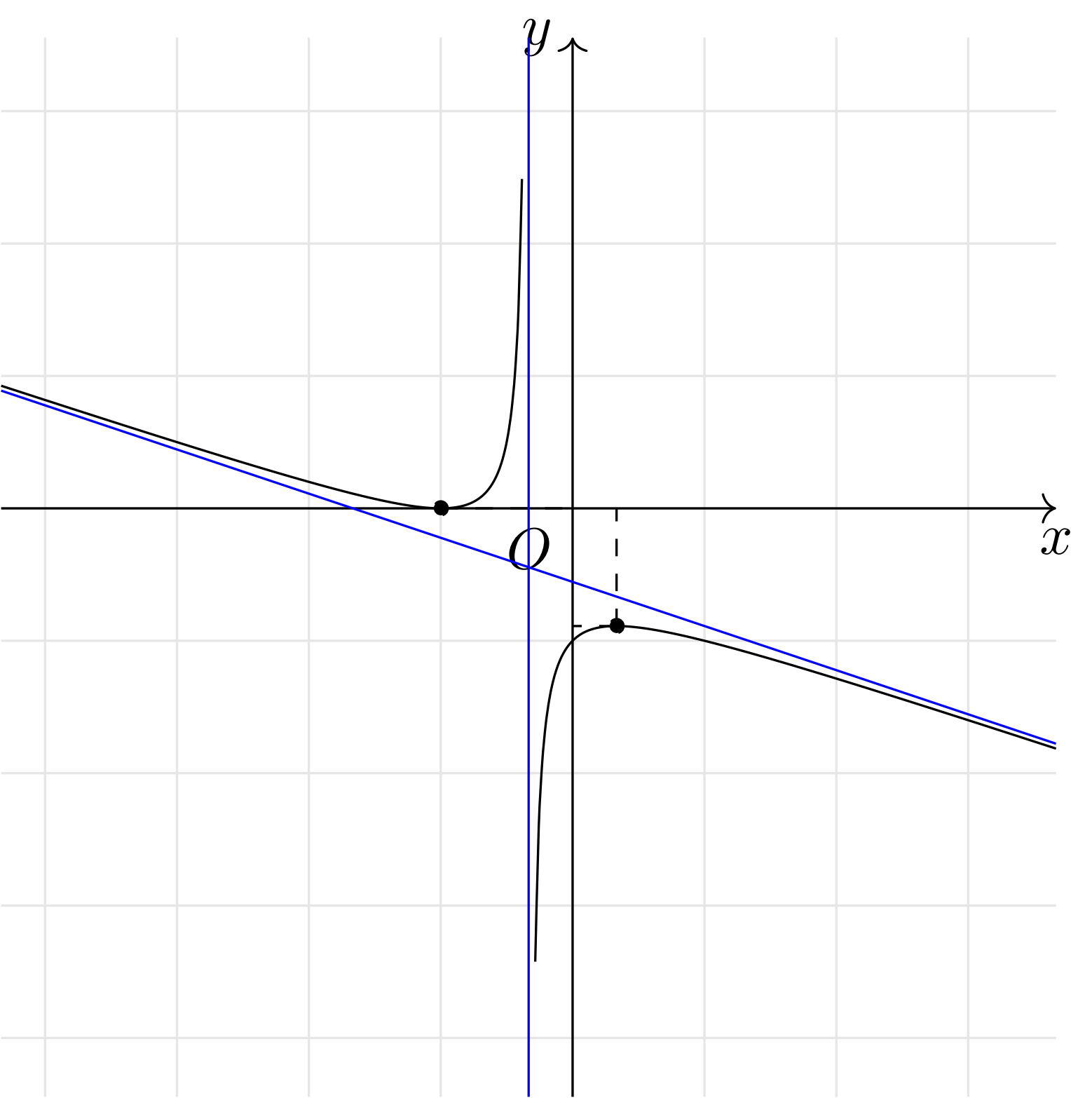
A. $y = -2x -1$.
B. $y = -x -2$.
C. $y = – \dfrac{4}{9}$.
D. $y = – \dfrac{x}{3} – \dfrac{5}{9}$.
Lời giải: Dựa vào đồ thị hàm số ta thấy tiệm cận xiên của đồ thị hàm số là $y = – \dfrac{x}{3} – \dfrac{5}{9}$
Phân tích và Phương pháp giải
Dạng bài toán yêu cầu xác định phương trình tiệm cận xiên của đồ thị hàm số. Trong bài toán gốc, tiệm cận xiên được xác định thông qua việc quan sát hành vi của đồ thị khi $x \to \pm\infty$. Đường thẳng mà đồ thị tiến sát tới chính là tiệm cận xiên $y = ax + b$. Đối với các hàm phân thức, tiệm cận xiên tồn tại khi bậc của tử số lớn hơn bậc của mẫu số đúng 1 đơn vị, và có thể tìm bằng cách thực hiện phép chia đa thức hoặc sử dụng công thức giới hạn.
Bài toán tương tự
Cho hàm số $y = f(x) = \frac{x^2 + 3x – 2}{x – 1}$. Khi đó, tiệm cận xiên của đồ thị hàm số là:A. $y = x + 2$.B. $y = x + 4$.C. $y = 2x – 1$.D. $y = x – 2$.Đáp án đúng: B.Lời giải ngắn gọn:Thực hiện phép chia đa thức tử số cho mẫu số:$$x^2 + 3x – 2 = (x – 1)(x + 4) + 2$$Do đó,$$\frac{x^2 + 3x – 2}{x – 1} = x + 4 + \frac{2}{x – 1}$$Vì $\lim_{x \to \pm\infty} \frac{2}{x – 1} = 0$, nên tiệm cận xiên của đồ thị hàm số là đường thẳng $y = x + 4$.
