Cho hàm số $y=f(x)=\dfrac{x^2+4x+4}{-x+5}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{-5\right\}$.

Bài toán gốc

Câu 20. Cho hàm số $y=f(x)=\dfrac{x^2+4x+4}{-x+5}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{-5\right\}$.

b) $y^{\prime}=\dfrac{-x^2+10x-24}{(-x+5)^2}$.

c) Hàm số $y=f(x)$ đạt điểm cực đại tại $x=12$.

d) Hàm số $y=f(5x+1)$ đạt cực tiểu tại điểm $x=\dfrac{11}{5}$.

Lời giải: $y^{\prime}=\dfrac{-x^2+10x+24}{(-x+5)^2}$.
$y^{\prime}=0\Leftrightarrow x_1=-2,x_2=12$.

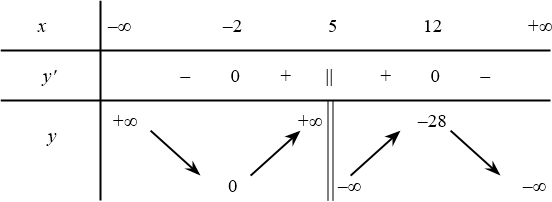
(Sai) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{-5\right\}$.
(Vì): $-x+5\neq 0\Leftrightarrow x\neq 5$ nên $D=\mathbb{R}\backslash \left\{5\right\}$.
(Sai) $y^{\prime}=\dfrac{-x^2+10x-24}{(-x+5)^2}$.
(Vì): $y^{\prime}=\dfrac{adx^2+2aex+be-cd}{(dx+e)^2}=\dfrac{-x^2+10x+24}{(-x+5)^2}$.
(Đúng) Hàm số $y=f(x)$ đạt điểm cực đại tại $x=12$.
(Sai) Hàm số $y=f(5x+1)$ đạt cực tiểu tại điểm $x=\dfrac{11}{5}$.
(Vì): $f^{\prime}(5x+1)=0\Rightarrow \left[\begin{array}{l} 5x+1=-2\text{ (CT) }\\ 5x+1=12\text{ (CĐ)} \end{array}\right.$
$\Leftrightarrow \left[\begin{array}{l} x=-\dfrac{3}{5}\text{ (CT) } \\ x=\dfrac{11}{5}\text{ (CĐ) } \end{array}\right.$.
Hàm số $y=f(x)$ và hàm số $y=f(ax+b)$ có cùng số điểm cực trị, cùng số điểm cực đại, cùng số điểm cực tiểu. Biến điểm cực đại thành điểm cực đại, biến điểm cực tiểu thành điểm cực tiểu. Có giá trị cực đại bằng nhau và giá trị cực tiểu bằng nhau tương ứng.

Phân tích và Phương pháp giải

Đây là dạng bài tập tổng hợp về khảo sát hàm số phân thức, bao gồm việc xác định tập xác định, tính đạo hàm bằng quy tắc thương, tìm điểm cực trị của hàm số $y=f(x)$ (bằng cách giải $y’=0$ và lập bảng biến thiên), và xác định các điểm cực trị của hàm hợp $y=f(ax+b)$. Điểm mấu chốt là nhận ra rằng các điểm cực trị của hàm $f(ax+b)$ được xác định bởi nghiệm của phương trình $ax+b = x_{CT/CD}$, trong đó $x_{CT/CD}$ là các điểm cực trị của $f(x)$.

Bài toán tương tự

Cho hàm số $y=f(x)=\dfrac{x^2-6x+9}{x+2}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{-2\right\}$.

b) $y^{\prime}=\dfrac{x^2+4x-21}{(x+2)^2}$.

c) Hàm số $y=f(x)$ đạt điểm cực đại tại $x=-7$.

d) Hàm số $y=f(2x-1)$ đạt cực tiểu tại điểm $x=2$.

Đáp án và Lời giải ngắn gọn:

1. Tập xác định: Mẫu số $x+2\neq 0 \Leftrightarrow x\neq -2$. Vậy $D=\mathbb{R}\backslash \left\{-2\right\}$. (Phát biểu a) Đúng).

2. Đạo hàm: Áp dụng quy tắc đạo hàm của hàm phân thức $y = u/v$:
$y^{\prime} = \dfrac{(2x-6)(x+2) – (x^2-6x+9)}{(x+2)^2} = \dfrac{(2x^2+4x-6x-12) – (x^2-6x+9)}{(x+2)^2} = \dfrac{x^2+4x-21}{(x+2)^2}$. (Phát biểu b) Đúng).

3. Cực trị của $f(x)$: $y’=0 \Leftrightarrow x^2+4x-21=0$. Giải ra ta được $x_1=-7$ và $x_2=3$.
Lập bảng biến thiên: $x=-7$ là điểm Cực đại, $x=3$ là điểm Cực tiểu. (Phát biểu c) Đúng).

4. Cực trị của $f(2x-1)$: Hàm số đạt cực tiểu khi $2x-1$ bằng điểm cực tiểu của $f(x)$, tức là $2x-1=3$.
$2x-1=3 \Leftrightarrow 2x=4 \Leftrightarrow x=2$. (Phát biểu d) Đúng).