Bài toán gốc
Câu 17. Hàm số $y=2x^3-6x^2-18x+5$. Xét tính đúng sai của các phát biểu sau:
a) Đồ thị hàm số đạt cực đại tại điểm $M(-1;15)$.
b) Tổng giá trị cực đại và cực tiểu của hàm số bằng 2.
c) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng $4\sqrt{257}$.
d) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=-16x-1$.
Lời giải: $y^{\prime}=6x^2-12x-18$
$y^{\prime}=0\Leftrightarrow x_1=-1,x_2=3$.
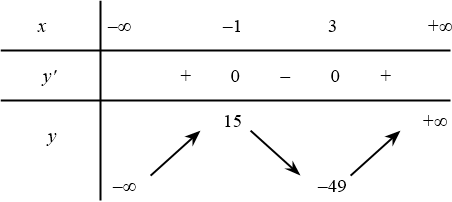
(Đúng) Đồ thị hàm số đạt cực đại tại điểm $M(-1;15)$.
(Sai) Tổng giá trị cực đại và cực tiểu của hàm số bằng 2.
(Vì): bằng $y_1+y_2=-34$.
(Đúng) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng $4\sqrt{257}$.
(Vì): $A(-1;15), B(3;-49)$. Khi đó $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=4\sqrt{257}$.
(Đúng) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=-16x-1$.
(Vì): gọi $A\left( {{x}_{1}};{{y}_{1}} \right),B\left( {{x}_{2}};{{y}_{2}} \right)$ là hai điểm cực trị của đồ thị hàm số thì đường thẳng $AB:y=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}\left( x-{{x}_{1}} \right)+{{y}_{1}}$.
Phân tích và Phương pháp giải
Đây là dạng bài toán khảo sát toàn diện các tính chất của cực trị hàm số bậc ba $y=ax^3+bx^2+cx+d$. Phương pháp giải bao gồm: 1) Tính đạo hàm $y’$. 2) Giải phương trình $y’=0$ để tìm hoành độ các điểm cực trị $x_1, x_2$. 3) Thay $x_1, x_2$ vào $y$ để tìm tọa độ các điểm cực trị $A(x_1, y_1)$ và $B(x_2, y_2)$. 4) Từ tọa độ này, tính toán các yêu cầu về giá trị cực trị, khoảng cách $AB$, và lập phương trình đường thẳng đi qua $A$ và $B$. (Để tìm nhanh phương trình đường thẳng đi qua hai điểm cực trị, ta thường chia $y$ cho $y’$ để lấy phần dư, hoặc dùng công thức $y=y'(x) rac{ax+b}{3a} + R(x)$, trong đó $R(x)$ là phương trình cần tìm.)
Bài toán tương tự
Cho hàm số $y=x^3-3x^2-9x+1$. Xét tính đúng sai của các phát biểu sau:
a) Đồ thị hàm số đạt cực tiểu tại $x=3$ và giá trị cực tiểu là $y_{CT}=-26$.
b) Tổng giá trị cực đại và cực tiểu của hàm số bằng $-20$.
c) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số là $4\sqrt{65}$.
d) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=-8x+10$.
Đáp án và Lời giải ngắn gọn:
Ta có $y’=3x^2-6x-9$.
$y’=0 \Leftrightarrow x=-1$ hoặc $x=3$.
Hoành độ cực trị là $x_1=-1$ (cực đại) và $x_2=3$ (cực tiểu).
$y_{CĐ} = y(-1) = 6$. Điểm cực đại $A(-1; 6)$.
$y_{CT} = y(3) = -26$. Điểm cực tiểu $B(3; -26)$.
a) (Đúng) Đồ thị hàm số đạt cực tiểu tại $x=3$ với $y_{CT}=-26$.
b) (Đúng) Tổng giá trị cực đại và cực tiểu: $6 + (-26) = -20$.
c) (Đúng) Khoảng cách $AB$: $AB = \sqrt{(3 – (-1))^2 + (-26 – 6)^2} = \sqrt{4^2 + (-32)^2} = \sqrt{16 + 1024} = \sqrt{1040} = 4\sqrt{65}$.
d) (Sai) Đường thẳng qua hai điểm cực trị $A(-1; 6)$ và $B(3; -26)$ có hệ số góc $m = \frac{-26 – 6}{3 – (-1)} = -8$. Phương trình đường thẳng là $y – 6 = -8(x – (-1)) \Rightarrow y = -8x – 2$. (Phát biểu d) sai vì nó ghi $y=-8x+10$.)
