Hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Xét tính đúng sai của các phát biểu sau:

Bài toán gốc

Câu 12. Hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

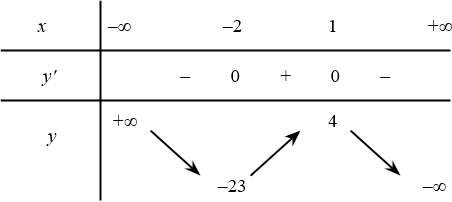
Xét tính đúng sai của các phát biểu sau:

a) Cực đại hàm số bằng $4$. b) Giá trị cực đại hàm số bằng $-23$.

c) Hàm số đạt cực tiểu tại điểm $x=1$. d) Cực tiểu hàm số bằng $-23$.

Lời giải:
(Đúng) Cực đại hàm số bằng $4$.
(Sai) Giá trị cực đại hàm số bằng $-23$.
(Sai) Hàm số đạt cực tiểu tại điểm $x=1$.
(Đúng) Cực tiểu hàm số bằng $-23$.

Phân tích và Phương pháp giải

Đây là dạng bài tập cơ bản về phân tích bảng biến thiên để xác định các yếu tố cực trị của hàm số. Phương pháp giải đòi hỏi việc nắm vững định nghĩa về Cực đại, Cực tiểu, Điểm cực đại/cực tiểu, và Giá trị cực đại/cực tiểu. Cụ thể: 1. Điểm cực trị là hoành độ (giá trị x) nơi đạo hàm đổi dấu. 2. Giá trị cực trị (Cực trị hàm số) là tung độ (giá trị y) tương ứng tại các điểm cực trị đó. Đạo hàm đổi dấu từ (+) sang (-) là cực đại, từ (-) sang (+) là cực tiểu.

Bài toán tương tự

Hàm số $y=f(x)$ có bảng biến thiên như sau:||$x$|$-\infty$|$-2$|$3$|$+\infty$|\n|—|—|—|—|—|\n|$f'(x)$|$-$|$0$|$+$|$0$|$-$|\n|$f(x)$|$+\infty \downarrow$|$-1$|$\uparrow 5 \downarrow$|$-\infty$|\nTrong các khẳng định sau, khẳng định nào là đúng?\nA. Giá trị cực tiểu của hàm số là $x=-2$.\nB. Hàm số đạt cực đại tại điểm $x=5$.\nC. Cực tiểu của hàm số bằng $-1$.\nD. Cực đại của hàm số bằng $3$.\n\nĐáp án đúng: C. \nLời giải ngắn gọn: Dựa vào bảng biến thiên, ta thấy:\n- Hàm số đạt cực tiểu tại điểm $x=-2$, và giá trị cực tiểu (cực tiểu hàm số) là $y=-1$. \n- Hàm số đạt cực đại tại điểm $x=3$, và giá trị cực đại (cực đại hàm số) là $y=5$. \nKiểm tra các phương án:\n- A sai, vì giá trị cực tiểu phải là giá trị $y$, tức là $-1$.\n- B sai, vì hàm số đạt cực đại tại $x=3$ (không phải $x=5$).\n- C đúng, Cực tiểu hàm số là giá trị $y$ nhỏ nhất tại chỗ đổi dấu đạo hàm, $y=-1$.\n- D sai, vì $3$ là điểm cực đại (giá trị $x$), còn cực đại hàm số là $5$ (giá trị $y$).