Hàm số $y=2x^3-3x^2-12x-3$. Xét tính đúng sai của các phát biểu sau:

Bài toán gốc

Câu 13. Hàm số $y=2x^3-3x^2-12x-3$. Xét tính đúng sai của các phát biểu sau:

a) Giá trị cực đại hàm số bằng $4$. b) Cực đại hàm số bằng $4$.

c) Cực tiểu hàm số bằng $2$. d) Hàm số đạt cực đại tại điểm $x=2$.

Lời giải: $y^{\prime}=6x^2-6x-12$
$y^{\prime}=0\Leftrightarrow x_1=-1,x_2=2$.

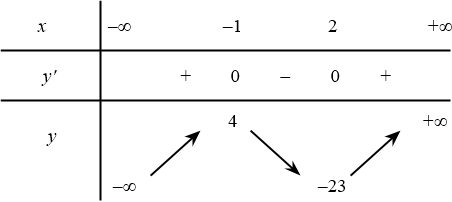
(Đúng) Giá trị cực đại hàm số bằng $4$.
(Đúng) Cực đại hàm số bằng $4$.
(Sai) Cực tiểu hàm số bằng $2$.
(Sai) Hàm số đạt cực đại tại điểm $x=2$.

Phân tích và Phương pháp giải

Bài toán yêu cầu xác định các điểm cực trị (x) và giá trị cực trị (y) của hàm số đa thức bậc ba, sau đó đánh giá tính đúng sai của các phát biểu liên quan. Phương pháp giải chung là: (1) Tính đạo hàm bậc nhất $y’$. (2) Giải phương trình $y’=0$ để tìm các điểm cực trị. (3) Lập bảng biến thiên hoặc sử dụng quy tắc xét dấu đạo hàm bậc hai (hoặc quy tắc 1) để xác định loại cực trị (cực đại/cực tiểu). (4) Tính các giá trị $y$ tương ứng. Điểm cần lưu ý là phân biệt rõ ràng giữa ‘giá trị cực đại’ ($y_{CĐ}$) và ‘điểm cực đại’ ($x_{CĐ}$).

Bài toán tương tự

Xét hàm số $y=x^3-6x^2+5$. Hãy xác định tính đúng sai của các phát biểu sau:

1. Hàm số đạt cực tiểu tại $x=4$.

2. Giá trị cực đại của hàm số bằng $5$.

3. Cực tiểu của hàm số là $5$.

4. Hàm số đạt cực đại tại điểm $x=0$.

Đáp án và Lời giải ngắn gọn:

Ta có $y’ = 3x^2 – 12x$. Cho $y’=0 \Leftrightarrow 3x(x-4)=0$. Các điểm cực trị là $x=0$ và $x=4$.

Bảng biến thiên cho thấy:

– Tại $x=0$, $y’$ đổi dấu từ dương sang âm $\Rightarrow$ Hàm số đạt cực đại. $y_{CĐ} = y(0) = 5$.

– Tại $x=4$, $y’$ đổi dấu từ âm sang dương $\Rightarrow$ Hàm số đạt cực tiểu. $y_{CT} = y(4) = 4^3 – 6(4^2) + 5 = 64 – 96 + 5 = -27$.

Đánh giá các phát biểu:

1. Đúng (Hàm số đạt cực tiểu tại $x=4$).

2. Đúng (Giá trị cực đại $y_{CĐ}=5$).

3. Sai (Cực tiểu là giá trị $y_{CT}=-27$, không phải $5$).

4. Đúng (Hàm số đạt cực đại tại điểm $x=0$ – là $x_{CĐ}$).