Ví dụ minh họa Cực trị của hàm số

Tìm cực trị của hàm số không có tham số

Ví dụ 1:

Tìm các điểm cực trị của các hàm số sau:

a) \(y = \frac{1}{3}{x^3} – {x^2} – 3x + \frac{4}{3}\)

b) \(y = \left| x \right|\left( {x + 2} \right)\)

Lời giải:

a)  \(y = \frac{1}{3}{x^3} – {x^2} – 3x + \frac{4}{3}\)

Cách 1:

• Hàm số có TXĐ: \(D=\mathbb{R}\)
• \(y’ = {x^2} – 2x – 3\)
• \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 3 \end{array} \right.\)
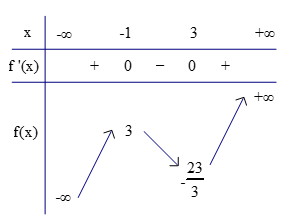
• Bảng biến thiên:

​

• Kết luận:
  • Hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\);
  • Hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).

Cách 2: 

• Hàm số có TXĐ: \(D=\mathbb{R}\)
• \(y’ = {x^2} – 2x – 3\)
• \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 3 \end{array} \right.\)
• \(y ”= 2x – 2\)
  •  \(y”\left( { – 1} \right) = – 4 < 0\) suy ra hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\).
  • ​\(y”\left( 3 \right) = 4 > 0\) suy ra hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).

b)  \(y = \left| x \right|\left( {x + 2} \right)\)

• Hàm số có TXĐ: \(D=\mathbb{R}\)
• \(y’ = \frac{x}{{\left| x \right|}}\left( {x + 2} \right) + \left| x \right| = \frac{{2\left( {{x^2} + x} \right)}}{{\left| x \right|}} (x\ne0)\)
• Bảng biến thiên:

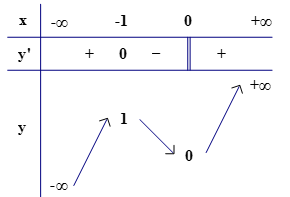
• Kết luận:
  • Hàm số đạt cực đại tại \(x=-1,\) giá trị cực đại tương ứng là \(y(-1)=1;\)
  • Hàm số đạt cực tiểu tại \(x=0,\) giá trị cực tiểu \(y(0)=0.\)

Ví dụ 2:

Tìm cực trị của hàm số \(y=x-sin2x+2.\)

Lời giải: 

• Hàm số có TXĐ: \(D=\mathbb{R}\)

• \(y’ = 1 – 2\cos 2x\)
• \(y’=0 \Leftrightarrow \cos2x\Leftrightarrow x = \pm \frac{\pi }{6} + k\pi (k\in\mathbb{Z})\)
• ​\(y” = 4\sin 2x\)
  • \(y”\left( {\frac{\pi }{6} + k\pi } \right) = 4\sin \left( {\frac{\pi }{3} + 2k\pi } \right) = 2\sqrt 3 > 0\) suy ra hàm số đạt cực tiểu tại \(x = \frac{\pi }{6} + k\pi\), giá trị cực tiểu tương ứng là \(y\left( {\frac{\pi }{6} + k\pi } \right) = {\textstyle{\pi \over 6}} + k\pi – \frac{{\sqrt 3 }}{2} + 2\).
  • ​\(y”\left( { – \frac{\pi }{6} + k\pi } \right) = 4\sin \left( { – \frac{\pi }{3} + 2k\pi } \right) = – 2\sqrt 3 < 0\) suy ra hàm số đạt cực đại tại \(x = -\frac{\pi }{6} + k\pi\), giá trị cực đại tương ứng là \(y\left( { – \frac{\pi }{6} + k\pi } \right) = – \frac{\pi }{6} + k\pi – \frac{{\sqrt 3 }}{2} + 2\).