Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Trắc nghiệm Khoảng cách và góc trong không gian

21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\).

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\). A. … [Đọc thêm...] về21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\).

15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá trị lớn nhất của thể tích khối chóp \(S.ABCD\) bằng 

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá … [Đọc thêm...] về15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá trị lớn nhất của thể tích khối chóp \(S.ABCD\) bằng 

35. Cho lăng trụ tam giác đều \(ABC.A’B’C’\) có cạnh đáy bằng \(a\) chiều cao bằng \(2a\). Mặt phẳng \(\left( P \right)\) qua \(B’\) và vuông góc với \(A’C\) chia lăng trụ thành hai khối đa diện. Biết thể tích của hai khối đa diện đó là \({V_1}\) và \({V_2}\) với \({V_1} < {V_2}\). Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 35. Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\) chiều cao bằng \(2a\). Mặt phẳng \(\left( P \right)\) qua \(B'\) và vuông góc với \(A'C\) chia lăng trụ thành hai khối đa diện. Biết thể tích của hai khối đa diện đó là \({V_1}\) và … [Đọc thêm...] về35. Cho lăng trụ tam giác đều \(ABC.A’B’C’\) có cạnh đáy bằng \(a\) chiều cao bằng \(2a\). Mặt phẳng \(\left( P \right)\) qua \(B’\) và vuông góc với \(A’C\) chia lăng trụ thành hai khối đa diện. Biết thể tích của hai khối đa diện đó là \({V_1}\) và \({V_2}\) với \({V_1} < {V_2}\). Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng

10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ}  = 2\overrightarrow {QD} \). Gọi \(V\), \(V’\) lần lượt là thể tích của khối chóp \(S.ABCD\) và khối tứ diện \(MNPQ\). Khi đó \(\frac{{V’}}{V}\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ}  = 2\overrightarrow {QD} \). Gọi … [Đọc thêm...] về10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ}  = 2\overrightarrow {QD} \). Gọi \(V\), \(V’\) lần lượt là thể tích của khối chóp \(S.ABCD\) và khối tứ diện \(MNPQ\). Khi đó \(\frac{{V’}}{V}\) bằng

Cho hình lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông tại \(A\). \(AB = a\), \(AC = a\sqrt 3 \), \(AA’ = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A’B’C’} \right)\) trung với trung điểm \(H\) của đoạn \(B’C’\). Khoảng cách giữa hai đường thẳng \(AA’\) và \(BC’\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:,

Cho hình lăng trụ \(ABC.A'B'C'\) có tam giác \(ABC\) vuông tại \(A\). \(AB = a\), \(AC = a\sqrt 3 \), \(AA' = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) trung với trung điểm \(H\) của đoạn \(B'C'\) (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng \(AA'\) và \(BC'\) bằng A. \(\frac{{a\sqrt 5 }}{3}\). B. \(\frac{{a\sqrt … [Đọc thêm...] vềCho hình lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông tại \(A\). \(AB = a\), \(AC = a\sqrt 3 \), \(AA’ = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A’B’C’} \right)\) trung với trung điểm \(H\) của đoạn \(B’C’\). Khoảng cách giữa hai đường thẳng \(AA’\) và \(BC’\) bằng

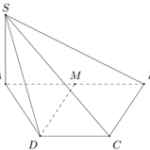
Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng. A. \(\frac{{3a}}{4}\). B. \(\frac{{3a}}{2}\). C. \(\frac{{3\sqrt {13} a}}{{13}}\). D. \(\frac{{6\sqrt … [Đọc thêm...] vềCâu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.

Đề: Trong không gian Oxyz, cho hai vectơ \(\vec u=\left( {1; – 2;1} \right)\)và \(\vec v=\left( { – 2;1;1} \right)\), góc giữa hai vecto đã cho bằng bao nhiêu?

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

==== Câu hỏi: Trong không gian Oxyz, cho hai vectơ \(\vec u=\left( {1; - 2;1} \right)\)và \(\vec v=\left( { - 2;1;1} \right)\), góc giữa hai vecto đã cho bằng bao nhiêu? A. \(\frac{\pi }{3}\) B. \(\frac{{2\pi }}{3}\) C. \(\frac{\pi }{6}\) D. \(\frac{{5\pi }}{6}\) Hãy chọn trả … [Đọc thêm...] vềĐề: Trong không gian Oxyz, cho hai vectơ \(\vec u=\left( {1; – 2;1} \right)\)và \(\vec v=\left( { – 2;1;1} \right)\), góc giữa hai vecto đã cho bằng bao nhiêu?

Đề: Trong không gian với hệ tọa độ Oxyz, cho hình lập phương ABCD.A'B'C'D' có \(A\left( {0;0;0} \right),B\left( {1;0;0} \right),D\left( {0;1;0} \right)\) và \(A'\left( {0;0;1} \right)\). Xét mặt phẳng (P) chứa CD’, gọi \(\alpha \) là góc giữa (P) và mặt phẳng \(\left( {BB'C'C} \right)\). Giá trị nhỏ nhất của \(\alpha \) là:

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

==== Câu hỏi: Trong không gian với hệ tọa độ Oxyz, cho hình lập phương ABCD.A'B'C'D' có \(A\left( {0;0;0} \right),B\left( {1;0;0} \right),D\left( {0;1;0} \right)\) và \(A'\left( {0;0;1} \right)\). Xét mặt phẳng (P) chứa CD’, gọi \(\alpha \) là góc giữa (P) và mặt phẳng \(\left( {BB'C'C} \right)\). Giá trị nhỏ nhất của \(\alpha \) là: A. … [Đọc thêm...] vềĐề: Trong không gian với hệ tọa độ Oxyz, cho hình lập phương ABCD.A'B'C'D' có \(A\left( {0;0;0} \right),B\left( {1;0;0} \right),D\left( {0;1;0} \right)\) và \(A'\left( {0;0;1} \right)\). Xét mặt phẳng (P) chứa CD’, gọi \(\alpha \) là góc giữa (P) và mặt phẳng \(\left( {BB'C'C} \right)\). Giá trị nhỏ nhất của \(\alpha \) là:

Đề: Trong không gian với hệ tọa độ Oxyz, cho \(A\left( { – 4;4;0} \right),B\left( {2;0;4} \right),C\left( {1;2; – 1} \right)\). Khoảng cách từ C đến đường thẳng AB là:

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

==== Câu hỏi: Trong không gian với hệ tọa độ Oxyz, cho \(A\left( { - 4;4;0} \right),B\left( {2;0;4} \right),C\left( {1;2; - 1} \right)\). Khoảng cách từ C đến đường thẳng AB là: A. 3 B. \(2\sqrt 2 \) C. \(3\sqrt 2 \) D. \(\sqrt {13} \) Hãy chọn trả lời đúng trước khi xem đáp … [Đọc thêm...] vềĐề: Trong không gian với hệ tọa độ Oxyz, cho \(A\left( { – 4;4;0} \right),B\left( {2;0;4} \right),C\left( {1;2; – 1} \right)\). Khoảng cách từ C đến đường thẳng AB là:

Đề: Trong không gian toạ độ Oxyz, cho mặt phẳng \((P): – 4x + 2y + 1 = 0\) và  điểm A(-1;0;1). Tính khoảng cách d từ A đến (P).

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

==== Câu hỏi: Trong không gian toạ độ Oxyz, cho mặt phẳng \((P): - 4x + 2y + 1 = 0\) và  điểm A(-1;0;1). Tính khoảng cách d từ A đến (P). A. \(d = \frac{1}{5}.\) B. \(d = 1\) C. \(d = \frac{8}{5}\) D. \(d = \frac{8}{{25}}\) Hãy chọn trả lời đúng trước khi xem đáp án và lời … [Đọc thêm...] vềĐề: Trong không gian toạ độ Oxyz, cho mặt phẳng \((P): – 4x + 2y + 1 = 0\) và  điểm A(-1;0;1). Tính khoảng cách d từ A đến (P).