Câu hỏi:
Cho hàm số \(y = f(x) = {e^{{x^2}}} + \sqrt[3]{{{x^4} - 1}}\). Xét các mệnh đề:
(I): Hàm số có tập xác định là \(D = [ - 1;1]\).
(II): Hàm số có tập xác định là \(D = \mathbb{R}\).
(III): Hàm số không có giá trị lớn nhất, giá trị nhỏ nhất.
(IV): Giá trị nhỏ nhất của hàm số bằng 0.
Số mệnh đề đúng là:
A. 1.
B. 4.
C. 3.
D. 2.
Lời … [Đọc thêm...] về Cho hàm số \(y = f(x) = {e^{{x^2}}} + \sqrt[3]{{{x^4} – 1}}\). Xét các mệnh đề: (I): Hàm số có tập xác định là \(D = [ – 1;1]\). (II): Hàm số có tập xác định là \(D = \mathbb{R}\). (III): Hàm số không có giá trị lớn nhất, giá trị nhỏ nhất. (IV): Giá trị nhỏ nhất của hàm số bằng 0. Số mệnh đề đúng là:
Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số
Gọi \(S\) là tập hợp tất cả các số nguyên \(m\) để hàm số \(y = \left| {\frac{1}{4}{x^4} – \frac{{19}}{2}{x^2} + 30x + m} \right|\) có giá trị lớn nhất trên đoạn \(\left[ {0\,;\,2} \right]\) không vượt quá \(20\). Số phần tử của tập hợp \(S\) bằng?
Câu hỏi:
Gọi \(S\) là tập hợp tất cả các số nguyên \(m\) để hàm số \(y = \left| {\frac{1}{4}{x^4} - \frac{{19}}{2}{x^2} + 30x + m} \right|\) có giá trị lớn nhất trên đoạn \(\left[ {0\,;\,2} \right]\) không vượt quá \(20\). Số phần tử của tập hợp \(S\) bằng?
A. 12.
B. 13.
C. 14.
D. 15.
Lời giải
Chọn D
Đặt \(f\left( x \right) = y = \left| {\frac{1}{4}{x^4} … [Đọc thêm...] về Gọi \(S\) là tập hợp tất cả các số nguyên \(m\) để hàm số \(y = \left| {\frac{1}{4}{x^4} – \frac{{19}}{2}{x^2} + 30x + m} \right|\) có giá trị lớn nhất trên đoạn \(\left[ {0\,;\,2} \right]\) không vượt quá \(20\). Số phần tử của tập hợp \(S\) bằng?
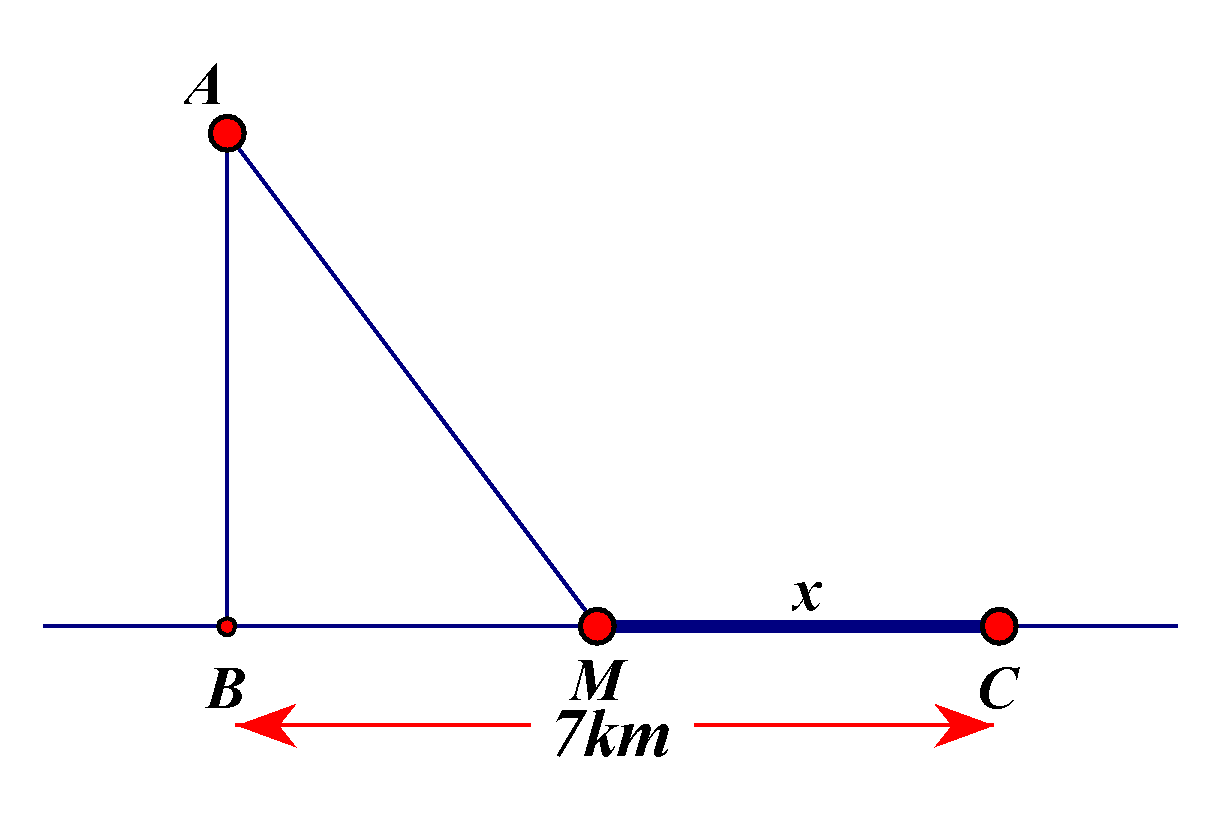
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {km} \right)\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng \(BC = 7\left( {km} \right)\). Người canh hải đăng phải chèo thuyền từ vị trí \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(6\left( {km/h} \right)\) rồi đi xe đạp từ \(M\) đến \(C\) với vận tốc \(10\left( {km/h} \right)\) (hình vẽ bên). Xác định khoảng cách từ \(M\) đến \(C\) để người đó đi từ \(A\) đến \(C\) là nhanh nhất.
 .
.
Câu hỏi:
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {km} \right)\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng \(BC = 7\left( {km} \right)\). Người canh hải đăng phải chèo thuyền từ vị trí \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(6\left( {km/h} \right)\) rồi đi xe đạp từ \(M\) đến \(C\) với vận tốc \(10\left( … [Đọc thêm...] về Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {km} \right)\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng \(BC = 7\left( {km} \right)\). Người canh hải đăng phải chèo thuyền từ vị trí \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(6\left( {km/h} \right)\) rồi đi xe đạp từ \(M\) đến \(C\) với vận tốc \(10\left( {km/h} \right)\) (hình vẽ bên). Xác định khoảng cách từ \(M\) đến \(C\) để người đó đi từ \(A\) đến \(C\) là nhanh nhất..
Cho \(x\),\(y\),\(z\) là ba số thực thỏa mãn \(1 \le x \le y \le z \le 2\). Giá trị nhỏ nhất của biểu thức sau: \(H = \frac{{x + 3y}}{{{z^2} + 3\left( {x + y + 1} \right)}} + \frac{{y + 3z}}{{{x^2} + 3\left( {y + z + 1} \right)}} + \frac{{z + 3x}}{{{y^2} + 3\left( {z + x + 1} \right)}} + \frac{1}{{4\left( {x + y + z – 1} \right)}}\)
Câu hỏi:
Cho \(x\),\(y\),\(z\) là ba số thực thỏa mãn \(1 \le x \le y \le z \le 2\). Giá trị nhỏ nhất của biểu thức sau: \(H = \frac{{x + 3y}}{{{z^2} + 3\left( {x + y + 1} \right)}} + \frac{{y + 3z}}{{{x^2} + 3\left( {y + z + 1} \right)}} + \frac{{z + 3x}}{{{y^2} + 3\left( {z + x + 1} \right)}} + \frac{1}{{4\left( {x + y + z - 1} \right)}}\)
A. \(\frac{{53}}{{40}}\).
B. … [Đọc thêm...] về Cho \(x\),\(y\),\(z\) là ba số thực thỏa mãn \(1 \le x \le y \le z \le 2\). Giá trị nhỏ nhất của biểu thức sau: \(H = \frac{{x + 3y}}{{{z^2} + 3\left( {x + y + 1} \right)}} + \frac{{y + 3z}}{{{x^2} + 3\left( {y + z + 1} \right)}} + \frac{{z + 3x}}{{{y^2} + 3\left( {z + x + 1} \right)}} + \frac{1}{{4\left( {x + y + z – 1} \right)}}\)
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{{x^2} – 8x}}{{x + 1}}\) trên đoạn \(\left[ {1\,;3} \right]\). Khi đó \(M – m\) bằng
Câu hỏi:
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{{x^2} - 8x}}{{x + 1}}\) trên đoạn \(\left[ {1\,;3} \right]\). Khi đó \(M - m\) bằng
A. \( - 3\).
B. \(\frac{1}{2}\).
C. \(\frac{{26}}{5}\).
D. \(\frac{{24}}{5}\).
Lời giải
Chọn B
Xét hàm số \(f\left( x \right) = \frac{{{x^2} - 8x}}{{x + 1}}\) trên … [Đọc thêm...] về Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{{x^2} – 8x}}{{x + 1}}\) trên đoạn \(\left[ {1\,;3} \right]\). Khi đó \(M – m\) bằng
Gọi \(M\), \(m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \left| { – {x^3} + 3{x^2} – 3} \right|\) trên đoạn \(\left[ {1\,;\,3} \right]\). Khi đó \(M + m\) nằm trong khoảng nào?
Câu hỏi:
Gọi \(M\), \(m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \left| { - {x^3} + 3{x^2} - 3} \right|\) trên đoạn \(\left[ {1\,;\,3} \right]\). Khi đó \(M + m\) nằm trong khoảng nào?
A. \(\left( {2\,;\,4} \right)\).
B. \(\left( {0\,;\,1} \right)\).
C. \(\left( {1\,;\,2} \right)\).
D. \(\left( {3\,;\,5} \right)\).
Lời giải
Chọn … [Đọc thêm...] về Gọi \(M\), \(m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \left| { – {x^3} + 3{x^2} – 3} \right|\) trên đoạn \(\left[ {1\,;\,3} \right]\). Khi đó \(M + m\) nằm trong khoảng nào?
Cho hai số thực \(a\), \(b\) đều lớn hơn \(1\). Giá trị nhỏ nhất của biểu thức \(S = \frac{1}{{{{\log }_{ab}}a}} + \frac{1}{{{{\log }_{\sqrt[4]{{ab}}}}b}}\) bằng
Câu hỏi:
Cho hai số thực \(a\), \(b\) đều lớn hơn \(1\). Giá trị nhỏ nhất của biểu thức \(S = \frac{1}{{{{\log }_{ab}}a}} + \frac{1}{{{{\log }_{\sqrt[4]{{ab}}}}b}}\) bằng
A. \(\frac{4}{9}\).
B. \(\frac{9}{4}\).
C. \(\frac{9}{2}\).
D. \(\frac{1}{4}\).
Lời giải
Chọn B
Ta có \(S = \frac{1}{{{{\log }_{ab}}a}} + \frac{1}{{{{\log }_{\sqrt[4]{{ab}}}}b}}\)\( = … [Đọc thêm...] về Cho hai số thực \(a\), \(b\) đều lớn hơn \(1\). Giá trị nhỏ nhất của biểu thức \(S = \frac{1}{{{{\log }_{ab}}a}} + \frac{1}{{{{\log }_{\sqrt[4]{{ab}}}}b}}\) bằng
Cho hàm số \(y = \frac{{\sin x + {m^2}}}{{\sin x – 2}}\). Giá trị của \(m\) thuộc khoảng nào sau đây thì hàm số đạt giá trị lớn nhất là \( – 1\).
Câu hỏi:
Cho hàm số \(y = \frac{{\sin x + {m^2}}}{{\sin x - 2}}\). Giá trị của \(m\) thuộc khoảng nào sau đây thì hàm số đạt giá trị lớn nhất là \( - 1\).
A. \(\left( { - 1;0} \right)\).
B. \(\left( { - 4;3} \right)\).
C. \(\left( {4;6} \right)\).
D. \(\left( {0;1} \right)\).
Lời giải
Chọn B
Đặt \(t = \sin x,\,\left( {t \in \left[ { - 1;1} \right]} … [Đọc thêm...] về Cho hàm số \(y = \frac{{\sin x + {m^2}}}{{\sin x – 2}}\). Giá trị của \(m\) thuộc khoảng nào sau đây thì hàm số đạt giá trị lớn nhất là \( – 1\).
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{2\sin x + 3}}{{\sin x + 1}}\) trên đoạn \(\left[ {0\,;\,\frac{\pi }{2}} \right]\). Khi đó \({M^2} + {m^2}\) là
Câu hỏi:
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{2\sin x + 3}}{{\sin x + 1}}\) trên đoạn \(\left[ {0\,;\,\frac{\pi }{2}} \right]\). Khi đó \({M^2} + {m^2}\) là
A. \(\frac{{11}}{2}\).
B. \(\frac{{31}}{2}\).
C. \(15\).
D. \(\frac{{61}}{4}\).
Lời giải
Chọn D
Đặt \(t = \sin x\). Với \(x \in \left[ {0\,;\,\frac{\pi … [Đọc thêm...] về Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{2\sin x + 3}}{{\sin x + 1}}\) trên đoạn \(\left[ {0\,;\,\frac{\pi }{2}} \right]\). Khi đó \({M^2} + {m^2}\) là
Cho các số thực dương \(x,y\) thỏa mãn\({\log _{\frac{1}{2}}}x\, + \,{\log _{\frac{1}{2}}}y\,\, \le \,\,{\log _{\frac{1}{2}}}\left( {x + {y^2}} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là
Câu hỏi:
Cho các số thực dương \(x,y\) thỏa mãn\({\log _{\frac{1}{2}}}x\, + \,{\log _{\frac{1}{2}}}y\,\, \le \,\,{\log _{\frac{1}{2}}}\left( {x + {y^2}} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là
A. 9.
B. 8.
C. \(\frac{{25\sqrt 2 }}{4}\).
D. \(\frac{{17}}{2}\).
Lời giải
Chọn A
Ta có: \({\log _{\frac{1}{2}}}x\, + \,{\log … [Đọc thêm...] về Cho các số thực dương \(x,y\) thỏa mãn\({\log _{\frac{1}{2}}}x\, + \,{\log _{\frac{1}{2}}}y\,\, \le \,\,{\log _{\frac{1}{2}}}\left( {x + {y^2}} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là
