Một phầm mềm nhận dạng tin nhắn quãng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng, người ta thấy rằng trong số tất cả tin nhắn gửi đến, có $20%$ số tin nhắn bị đánh dấu. Trong số các tin nhắn bị đánh dấu, có $10%$ số tin nhắn không phải quảng cáo. Trong các tin nhắn không bị đánh dấu, có $10%$ số tin … [Đọc thêm...] vềMột phầm mềm nhận dạng tin nhắn quãng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng
Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số
Trong 9 giây đầu tiên, một chất điểm chuyển động theo phương trình
$s\left( t \right)=-{{t}^{3}}+9{{t}^{2}}+21t+1,$ trong đó $t$ tính bằng giây và $s$ tính bằng mét.
Trong 9 giây đầu tiên, một chất điểm chuyển động theo phương trình $s\left( t \right)=-{{t}^{3}}+9{{t}^{2}}+21t+1,$ trong đó $t$ tính bằng giây và $s$ tính bằng mét.a) $s'\left( t \right)=-3{{t}^{2}}+18t+21.$.b) $s''\left( t \right)=-6t+17.$.c) Phương trình $s'\left( t \right)=0$ có đúng một nghiệm dương là $t=7.$.d) Gia tốc của chất điểm tại thời điểm vật dừng lại là $-24$ … [Đọc thêm...] vềTrong 9 giây đầu tiên, một chất điểm chuyển động theo phương trình
$s\left( t \right)=-{{t}^{3}}+9{{t}^{2}}+21t+1,$ trong đó $t$ tính bằng giây và $s$ tính bằng mét.
Một tấm kẽm hình vuông $ABCD$ có cạnh bằng $30\ \text{cm}$. Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.
Một tấm kẽm hình vuông $ABCD$ có cạnh bằng $30\ \text{cm}$. Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. a) Thể tích khối lăng trụ được tính bằng công thức $V=30S$, trong đó $S$ là diện tích của tam giác $AEG$.b) Diện tích của tam giác $AEG$ bằng: $\sqrt{15}.\sqrt{{{\left( 15-x … [Đọc thêm...] vềMột tấm kẽm hình vuông $ABCD$ có cạnh bằng $30\ \text{cm}$. Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.
Người ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho trên Hình 1
Người ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho trên Hình 1. a) Có thể biểu thị $y$ theo công thức $y=2-\dfrac{\left( \pi +2 \right)x}{2}$.b) Diện tích của cửa sổ được tính bởi công thức $S\left( x \right)=4x-2{{x}^{2}}-\pi {{x}^{2}}\left( {{\text{m}}^{2}} … [Đọc thêm...] vềNgười ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho trên Hình 1
Tìm giá trị lớn nhất của hàm số $f(x) = 3 + 3x – e^x$ trên đoạn $[0; 5]$
Bài toán gốc Tìm giá trị lớn nhất của hàm số $f(x) = 3 + 3x - e^x$ trên đoạn $[0; 5]$A. $\max\limits_{\left[0; 5\right]} f(x) = 18 - e^{5}$.B. $\max\limits_{\left[0; 5\right]} f(x) = \ln{\left(27 \right)}$.C. $\max\limits_{\left[0; 5\right]} f(x) = 15$.D. $\max\limits_{\left[0; 5\right]} f(x) = 3\sqrt{5}$.Lời giải: Trên đoạn $[0; 5]$ ta có $f^{\prime}(x) = 3 - e^{x}$. … [Đọc thêm...] vềTìm giá trị lớn nhất của hàm số $f(x) = 3 + 3x – e^x$ trên đoạn $[0; 5]$
Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây:
Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[2;7]$ bằng

Bài toán gốc Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây:Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[2;7]$ bằng A. $f(2)$.B. $f(7)$.C. $f(0)$.D. $f(4)$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất/nhỏ nhất của hàm số $f(x)$ trên một đoạn $[a; b]$, trong đó thông tin được cung cấp dưới dạng … [Đọc thêm...] vềHàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây:

Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[2;7]$ bằng
Hàm số $y=f(x)$ có $y=f^{\prime}(x)=ax^2+bx+c$ có đồ thị như hình dưới đây: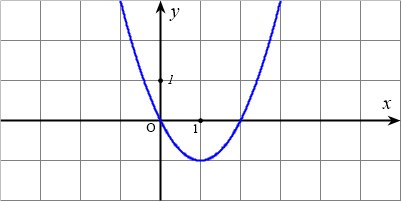
Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[1;3]$ bằng

Bài toán gốc Hàm số $y=f(x)$ có $y=f^{\prime}(x)=ax^2+bx+c$ có đồ thị như hình dưới đây:Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[1;3]$ bằngA. $f(1)$.B. $f(0)$.C. $f(3)$.D. $f(2)$.Lời giải: $y^{\prime}=x^2-2x$ Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên một đoạn $[a; b]$ dựa vào … [Đọc thêm...] vềHàm số $y=f(x)$ có $y=f^{\prime}(x)=ax^2+bx+c$ có đồ thị như hình dưới đây:

Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[1;3]$ bằng
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x \sqrt{225 – x^2}$
Bài toán gốc Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x \sqrt{225 - x^2}$A. $\max\limits_{\left[-15; 15\right]} f(x) = \dfrac{225}{2}$; $\min\limits_{\left[ -15; 15 \right]} f(x) = - \dfrac{225}{2}$.B. $\max\limits_{\left[-15; 15 \right]} f(x) = 0$; $\min\limits_{\left[ -15; 15 \right]} f(x) = - \dfrac{225}{2}$.C. $\max\limits_{\left[-15; 15 \right]} … [Đọc thêm...] vềTìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x \sqrt{225 – x^2}$
Mỗi trang giấy của một cuốn sách được qui định diện tích là 460 cm$^2$
Bài toán gốc Mỗi trang giấy của một cuốn sách được qui định diện tích là 460 cm$^2$. Khi trình bày nội dung lên trang giấy này người ta phải chừa trống lề trên và lề dưới là 3cm, lề trái và lề phải là 2cm. Biết diện tích của phần trình bày nội dung trang giấy có diện tích lớn nhất là $a-\sqrt{b}$. Tính $a+b$.A. $44644$.B. $44647$.C. $44641$.D. $44643$.Lời giải: Đặt … [Đọc thêm...] vềMỗi trang giấy của một cuốn sách được qui định diện tích là 460 cm$^2$
Hàm số $y=f(x)=-x^3+3x+2+m$, gọi giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên $[-3;3]$ lần lượt là $a,b$. Tìm $m$ để $a+b=6$?
Bài toán gốc Hàm số $y=f(x)=-x^3+3x+2+m$, gọi giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên $[-3;3]$ lần lượt là $a,b$. Tìm $m$ để $a+b=6$?A. $1$.B. $2$.C. $0$.D. $-2$.Lời giải: $y(-1)=0+m,y(1)=4+m,y(-3)=20+m,y(3)=-16+m$ Phân tích và Phương pháp giải Đây là dạng toán tìm tham số m dựa trên điều kiện liên quan đến giá trị lớn nhất (GTLN) và … [Đọc thêm...] vềHàm số $y=f(x)=-x^3+3x+2+m$, gọi giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên $[-3;3]$ lần lượt là $a,b$. Tìm $m$ để $a+b=6$?
