Một tấm kẽm hình vuông $ABCD$ có cạnh bằng $30\ \text{cm}$. Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.

Một tấm kẽm hình vuông $ABCD$ có cạnh bằng $30\ \text{cm}$. Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.

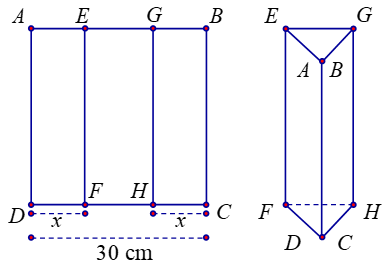
a) Thể tích khối lăng trụ được tính bằng công thức $V=30S$, trong đó $S$ là diện tích của tam giác $AEG$.

b) Diện tích của tam giác $AEG$ bằng: $\sqrt{15}.\sqrt{{{\left( 15-x \right)}^{2}}\left( 2x-15 \right)}$.

c) Giá trị của $x$ để thể tích khối lăng trụ lớn nhất là $x=12\left( \text{cm} \right)$.

d) Thể tích khối lăng trụ lớn nhất bằng $3750\left( c{{m}^{3}} \right)$.

Lời giải: 3

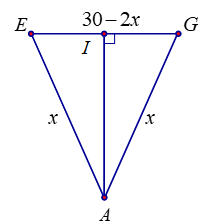
(a) Đúng: Đường cao lăng trụ là $AD=AB=30\ \text{cm}$ không đổi. Để thể tích lăng trụ lớn nhất chỉ cần diện tích đáy lớn nhất.
Gọi $I$ là trung điểm cạnh $EG$ $\Rightarrow AI\bot EG$ trong tam giác $AEG$
$\Rightarrow IG=15-x$

Ta có: $AI=\sqrt{{{x}^{2}}-{{\left( \dfrac{30-2x}{2} \right)}^{2}}}=\sqrt{{{x}^{2}}-{{\left( 15-x \right)}^{2}}}$ $=\sqrt{30x-225},x\in \left( \dfrac{15}{2};15 \right)$.
(b) Sai: ${{S}_{\Delta AEG}}=\dfrac{1}{2}AI \cdot EG=\dfrac{1}{2}\left( 30-2x \right)\sqrt{30x-225}$ $=\sqrt{15}\cdot\sqrt{{{\left( 15-x \right)}^{2}}\left( 2x-15 \right)}$
Vậy ta cần tìm $x\in \left( \dfrac{15}{2};15 \right)$ để $f\left( x \right)={{\left( 15-x \right)}^{2}}\left( 2x-15 \right)$ lớn nhất.
${f}’\left( x \right)=-2\left( 15-x \right)\left( 2x-15 \right)+2{{\left( 15-x \right)}^{2}}=2\left( 15-x \right)\left( 30-3x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=15 \\ x=10 \end{array} \right]$.
Bảng biến thiên:

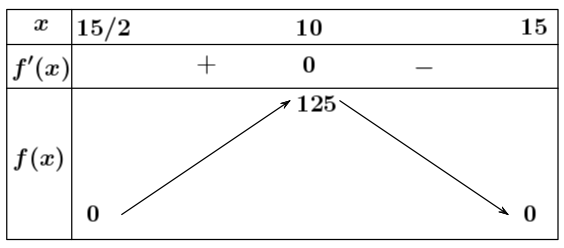
(c) Đúng: Vậy thể tích lăng trụ lớn nhất khi $x=10$.
(d) Sai: Và thể tích lớn nhất bằng $125 \cdot 30=3750\left( \text{cm}^{3} \right)$
(Đúng) Thể tích khối lăng trụ được tính bằng công thức $V=30S$, trong đó $S$ là diện tích của tam giác $AEG$.
(Vì): Chiều cao của lăng trụ là $30\ \text{cm}$. Diện tích đáy là $S$. Do đó, thể tích khối lăng trụ là $V=30S$.
(Đúng) Diện tích của tam giác $AEG$ bằng: $\sqrt{15}.\sqrt{{{\left( 15-x \right)}^{2}}\left( 2x-15 \right)}$.
(Vì): Diện tích của tam giác $AEG$ là ${{S}_{\Delta AEG}}=\dfrac{1}{2}AI \cdot EG=\dfrac{1}{2}\left( 30-2x \right)\sqrt{{{x}^{2}}-{{\left( 15-x \right)}^{2}}}=\dfrac{1}{2}\left( 30-2x \right)\sqrt{30x-225}=\sqrt{15}\cdot\sqrt{{{\left( 15-x \right)}^{2}}\left( 2x-15 \right)}$.
(Sai) Giá trị của $x$ để thể tích khối lăng trụ lớn nhất là $x=12\left( \text{cm} \right)$.
(Vì): Để thể tích khối lăng trụ lớn nhất, ta cần tìm giá trị $x$ sao cho hàm số $f\left( x \right)={{\left( 15-x \right)}^{2}}\left( 2x-15 \right)$ đạt giá trị lớn nhất. Ta có ${f}’\left( x \right)=0\Leftrightarrow x=10$ hoặc $x=15$. Từ bảng biến thiên, $f(x)$ đạt cực đại khi $x=10$.
(Đúng) Thể tích khối lăng trụ lớn nhất bằng $3750\left( c{{m}^{3}} \right)$.
(Vì): Giá trị lớn nhất của $f\left( x \right)={{\left( 15-x \right)}^{2}}\left( 2x-15 \right)$ tại $x=10$ là $f\left( 10 \right)={{(15-10)}^{2}}(2 \cdot 10-15)={{5}^{2}} \cdot 5=125$. Thể tích khối lăng trụ lớn nhất là $V=30 \cdot 125 = 3750\left( \text{cm}^{3} \right)$.