Người ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho trên Hình 1.
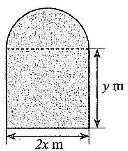
a) Có thể biểu thị $y$ theo công thức $y=2-\dfrac{\left( \pi +2 \right)x}{2}$.
b) Diện tích của cửa sổ được tính bởi công thức $S\left( x \right)=4x-2{{x}^{2}}-\pi {{x}^{2}}\left( {{\text{m}}^{2}} \right)$.
c) Diện tích của cửa sổ lớn nhất khi $x=\dfrac{4}{\pi +2}\left( \text{ m} \right)$.
d) Giá trị lớn nhất của diện sổ là $\dfrac{16}{\pi +4}\left( {{\text{m}}^{2}} \right)$.
Lời giải: Ta có $2x+2y+\pi x=4$, suy ra $y=2-\dfrac{\left( \pi +2 \right)x}{2}$.
$S\left( x \right)=2xy+\dfrac{\pi {{x}^{2}}}{2}=2x\left( 2-x-\dfrac{\pi x}{2} \right)+\dfrac{\pi {{x}^{2}}}{2}=4x-2{{x}^{2}}-\dfrac{\pi {{x}^{2}}}{2}\left( {{\text{m}}^{2}} \right)$.
Ta có $x{>}0$ và $y{>}0$, suy ra $0{<}x{
${S}’\left( x \right)=4-4x-\pi x;{S}’\left( x \right)=0\Leftrightarrow x=\dfrac{4}{\pi +4}$.
Bảng biến thiên:
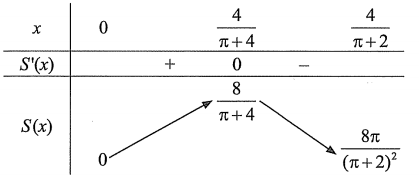
(Đúng) Có thể biểu thị $y$ theo công thức $y=2-\dfrac{\left( \pi +2 \right)x}{2}$.
(Vì): Ta có chu vi khung viền là $2y + 2x + \pi x = 4$. Suy ra $2y = 4 – 2x – \pi x \Rightarrow y = 2 – x – \dfrac{\left( \pi \right)x}{2} = 2 – \dfrac{\left( 2 + \pi \right)x}{2}$.
(Sai) Diện tích của cửa sổ được tính bởi công thức $S\left( x \right)=4x-2{{x}^{2}}-\pi {{x}^{2}}\left( {{\text{m}}^{2}} \right)$.
(Vì): Diện tích hình chữ nhật là $2xy$. Diện tích nửa hình tròn là $\dfrac{1}{2}\pi {{x}^{2}}$. Thay $y=2-\dfrac{\left( 2+\pi \right)x}{2}$ vào công thức diện tích ta được $S\left( x \right)=2x\left( 2-x-\dfrac{\pi x}{2} \right)+\dfrac{\pi {{x}^{2}}}{2}=4x-2{{x}^{2}}-\pi {{x}^{2}}+\dfrac{\pi {{x}^{2}}}{2}=4x-2{{x}^{2}}-\dfrac{\pi {{x}^{2}}}{2}$.
(Sai) Diện tích của cửa sổ lớn nhất khi $x=\dfrac{4}{\pi +2}\left( \text{ m} \right)$.
(Sai) Giá trị lớn nhất của diện sổ là $\dfrac{16}{\pi +4}\left( {{\text{m}}^{2}} \right)$.
(Vì): Giá trị lớn nhất của diện tích cửa sổ là $S\left( \dfrac{4}{\pi +4} \right)=\dfrac{8}{\pi +4}$.
