Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số

Một vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây và ${s}$ là quãng đường chuyển động được của vật trong ${t}$ giây tính bằng mét. Khi đó:a) Vận tốc của vật tại thời điểm ${t=2}$ là ${v(2)=s^{\prime}(2)=8({m} / {s})}$.b) Gia tốc của vật tại thời điểm ${t=2}$ là … [Đọc thêm...] vềMột vật chuyển động trên đường thẳng được xác định bởi công thức $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+7t-2$, trong đó ${t{>}0}$ và tính bằng giây và ${s}$ là quãng đường chuyển động được của vật trong ${t}$ giây tính bằng mét

Một tấm nhôm hình vuông cạnh $120cm$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( cm \right)$, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. a) Thể tích khối hộp nhận được khi tính theo $x$ là $V=x{{\left( 120-2x \right)}^{2}}$.b) Để hộp nhận được có thể tích lớn nhất thì $x=10\left( cm … [Đọc thêm...] vềMột tấm nhôm hình vuông cạnh $120cm$

Khi nuôi tôm thẻ trong ao, một kỹ sư thủy sản đã thống kê được nếu mỗi mét vuông mặt ao thả $x$ con tôm giống thì cuối mỗi vụ con tôm có cân nặng trung bình là $108-{{x}^{2}}$.a) Để lượng tôm thu được tăng lên thì mật độ tôm giống thả vào ao là từ 6 đến 10 con/ ${{m}^{2}}$.b) Sau mỗi vụ khối lượng tôm trung bình trong mỗi mét vuông mặt ao là $\left( 108-{{x}^{2}} \right)x$.c) … [Đọc thêm...] vềKhi nuôi tôm thẻ trong ao, một kỹ sư thủy sản đã thống kê được nếu mỗi mét vuông mặt ao thả $x$ con tôm giống thì cuối mỗi vụ con tôm có cân nặng trung bình là $108-{{x}^{2}}$

Khi bỏ qua sức cản của không khí, độ cao của một vật thể sau thời gian t giây được phóng thẳng đứng lên trên từ điểm cách mặt đất $5$ mét với tốc độ ban đầu $39,2$ m/s là $h\left( t \right)=5+39,2t-4,9{{t}^{2}}$, hiều dương là chiều hướng từ dưới lên. Các mệnh đề sau đúng hay sai?a) Vật đạt độ cao lớn nhất bằng $83,4$ mét tại thời điểm $t=4$ giây.b) Khoảng thời gian vật ở độ … [Đọc thêm...] vềKhi bỏ qua sức cản của không khí, độ cao của một vật thể sau thời gian t giây được phóng thẳng đứng lên trên từ điểm cách mặt đất $5$ mét với tốc độ ban đầu $39,2$ m/s là $h\left( t \right)=5+39,2t-4,9{{t}^{2}}$, hiều dương là chiều hướng từ dưới lên

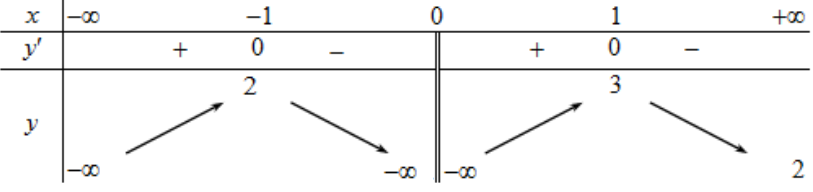
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau: a) Hàm số $y=f\left( x \right)$ nghịch biến trên $\left( 0;1 \right)$.b) Hàm số $y=f\left( x \right)$ đồng biến trên $\left( -\infty ;-1 \right)$.c) Hàm số $y=f\left( x \right)$ có 2 điểm cực trị.d) Giá trị lớn nhất của $g\left( x \right)=f\left( x \right)+\sin x$ trên đoạn $\left[ -\dfrac{\pi }{2};-1 \right]$ là … [Đọc thêm...] vềCho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

Chi phí nhiên liệu của một chiếc tầu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng $480$ nghìn đồng trên $1$ giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi $v=10$ thì phần thứ hai bằng $30$ nghìn đồng/giờ. Xét tính đúng sai của các mệnh đề sau:a) Khi vận tốc $v=10$ thì chi phí nguyên liệu cho phần thứ nhất trên $1km$ … [Đọc thêm...] vềChi phí nhiên liệu của một chiếc tầu chạy trên sông được chia làm hai phần

Một cơ sở đóng giầy sản xuất mỗi ngày được $x$ đôi giầy. $1\le x\le 20$. Tổng chi phí sản xuất $x$ đôi giầy là $C\left( x \right)={{x}^{3}}-6{{x}^{2}}-88x+592$. Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá $200$ nghìn đồng /một đôi. Gọi $T\left( x \right)$ là số tiền bán được và $L\left( x \right)$ là lợi nhuận thu được sau khi bán hết $x$ đôi giầy. Các mệnh đề sau đúng … [Đọc thêm...] vềMột cơ sở đóng giầy sản xuất mỗi ngày được $x$ đôi giầy