Thể tích nước của một bể bơi sau $t$ phút bơm tính theo công thức $V\left(t\right)=\dfrac{1}{100}\left(30t^{3}-\dfrac{t^{4}}{4}\right)$ (lít) với $\left(0\leq t\leq 90\right)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi công thức $f\left(t\right)=V’\left(t\right)$.

ĐỀ BÀI
Thể tích nước của một bể bơi sau $t$ phút bơm tính theo công thức $V\left(t\right)=\dfrac{1}{100}\left(30t^{3}-\dfrac{t^{4}}{4}\right)$
(lít) với $\left(0\leq t\leq 90\right)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi công thức $f\left(t\right)=V’\left(t\right)$.

Lời giải
a) Thể tích nước của bể bơi sau 20 phút bơm là 2000 lít
b) Tốc độ bơm nước tại thời điểm $t$ là $f\left(t\right)=90t^{2}-t^{3}$
c) Tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90
d) Tốc độ bơm lớn nhất tại thời điểm $t=60$ phút
Lời giải
a) Đúng: $V\left(20\right)=\dfrac{1}{100}\left(30.20^{3}-\dfrac{20^{4}}{4}\right)=2000$.
b) Sai: $V’\left(t\right)=\dfrac{1}{100}\left(90t^{2}-t^{3}\right)\Rightarrow f\left(t\right)=\dfrac{1}{100}\left(90t^{2}-t^{3}\right)$.
c) Đúng: $V”\left(t\right)=\dfrac{1}{100}\left(180t-3t^{2}\right)\Leftrightarrow V”\left(t\right)=0\Leftrightarrow \left[\begin{array}{*{20}{l}}t=60\\t=0\end{array}\right. $
Bảng biến thiên của hàm số:

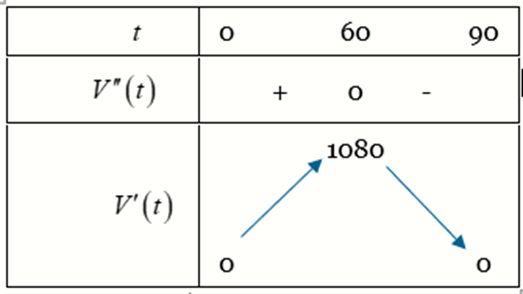
Suy ra tốc độ bơm giảm từ phút thứ 60 đến phút thứ 90 .
d) Đúng: Từ bảng biến thiên ta có tốc độ lớn nhất khi $t=60$ phút.