Hình vẽ dưới đây mô tả mặt cắt ngang của ngọn đuốc bằng kim loại được thiết kế cho một đại hội thể thao lớn. Ngọn đuốc có chiều cao $7,5\text{ }\!\!~\!\!\text{ m}$; mặt trên có chiều rộng 8 m ; mặt dưới có chiều rộng 2 m ; hai đường biên của ngọn đuốc đối xứng nhau qua trục $Oy$ và được cho bởi đường cong có phương trình $y=f\left( x \right)=a-\frac{b}{{{x}^{2}}}$ (đơn vị trên mỗi hệ trục tọa độ là mét)

ĐỀ BÀI
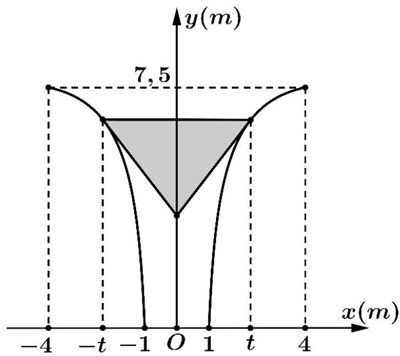
Hình vẽ dưới đây mô tả mặt cắt ngang của ngọn đuốc bằng kim loại được thiết kế cho một đại hội thể thao lớn. Ngọn đuốc có chiều cao $7,5\text{ }\!\!~\!\!\text{ m}$; mặt trên có chiều rộng 8 m ; mặt dưới có chiều rộng 2 m ; hai đường biên của ngọn đuốc đối xứng nhau qua trục $Oy$ và được cho bởi đường cong có phương trình $y=f\left( x \right)=a-\frac{b}{{{x}^{2}}}$ (đơn vị trên mỗi hệ trục tọa độ là mét)

Lời giải
a) $48a+50b=780$
b) Khoang bên trong của ngọn đuốc là một hình nón được minh họa bởi phần được tô đậm trong hình vẽ có độ dài đáy là $2t$ (mét), hai cạnh bên lần lượt nằm trên hai tiếp tuyến của đường cong cho bởi phương trình trên. Khi đó tiếp tuyến cắt trục $Oy$ tại tung độ theo $t$ là $\frac{8{{t}^{3}}-8t+16}{{{t}^{3}}}$
c) Thể tích của khối nón theo $t$ là $\frac{16\pi }{3t}$
d) Nhằm đảm bảo duy trì sức cháy của ngọn lửa trên ngọn đuốc đó, trên bề mặt hình nón người ta phủ lớp than sao cho toàn bộ không gian từ bề mặt hình nón đến đỉnh ngọn được lấp kín và thể tích phần than được sử dụng bằng thể tích khối nón. Khi đó, đỉnh khối nón cách đáy ngọn đuốc một khoảng bằng 8,4 mét.
Lời giải
a) Sai: Ta có $y=f\left( x \right)=a-\frac{b}{{{x}^{2}}}$ với đồ thị $f\left( x \right)$ đi qua 2 điểm $\left( 4;7,5 \right)$ và $\left( 1;0 \right)$.
DỄ dàng giải ra được $a=b=8$ tức $48a+50b=784$.
b) Sai: Do hình nón có độ dài đáy là $2t\left( m \right)$ nên hình nón có bán kính đáy $R$ bằng $t\left( m \right)\left( 1 \right)$ Đường sinh hình nón trùng với tiếp tuyến của $f\left( x \right)$ tại điểm $x=t$ nên ta có phương trình là:
$y={f}’\left( t \right)\left( x-t \right)+f\left( t \right)=\frac{16}{{{t}^{3}}}\left( x-t \right)+\left( 8-\frac{8}{{{t}^{2}}} \right)=\frac{16}{{{t}^{3}}}x+8-\frac{24}{{{t}^{2}}}.$
Thế $x=0$ ta suy ra tiếp tuyến cắt trục $Oy$ tại tung độ theo $t$ là: $8-\frac{24}{{{t}^{2}}}$.
c) Sai: Từ hình vẽ ta suy ra chiều cao hình nón là $h=\left| f\left( t \right)-\left( 8-\frac{24}{{{t}^{2}}} \right) \right|=\frac{16}{{{t}^{2}}}$
Từ (1) và (2) ta suy ra thể tích khối nón bằng $V=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{t}^{2}}\left( \frac{16}{{{t}^{2}}} \right)=\frac{16\pi }{3}$.
d) Sai: Trước hết ta cần biểu diễn lại hàm số $y=f\left( x \right)$ về lại hàm số $x=g\left( y \right)$.
Ta có: $y=8-\frac{8}{{{x}^{2}}}\Leftrightarrow \frac{8}{{{x}^{2}}}=8-y\Rightarrow x=g\left( y \right)=\sqrt{\frac{8}{8-y}}$ với $y<8$.
Khi đó thể tích phần chứa than là: ${{V}_{t}}=\pi \mathop{\int }_{t}^{7,5}{{g}^{2}}\left( y \right)dy=\pi \mathop{\int }_{t}^{7,5}\left( \frac{8}{8-y} \right)dy=\frac{16\pi }{3}$.
Phương trình tương đương với: $\mathop{\int }_{t}^{7,5}\left( \frac{8}{8-x} \right)dx=\frac{16}{3}\overset{\text{ }\!\!~\!\!\text{ SOLVE }\!\!~\!\!\text{ }}{\mathop{\to }}\,t=8\pm \frac{1}{2}{{e}^{\frac{2}{3}}}={{t}_{0}}$.
Suy ra khoảng cách cần tìm là: $8-{{\left. \frac{24}{{{t}^{2}}} \right|}_{t={{t}_{0}}}}\approx 7,07\left( \text{ }\!\!~\!\!\text{ m} \right)$