Một bể bơi hình trụ có đường kính 5 m và chiều cao 1 m ; bể được bơm nước vào với tốc độ không đổi $v_{0}$. Sau khi nước được bơm đầy, bể bơi bị thủng một lỗ ở đáy và nước chảy ra ngoài; bể bơi chảy hết nước trong 8 giờ. Biết tốc độ giảm chiều cao của bể bơi khi nước chảy ra ngoài vào thời điểm $t$ giờ (tính từ lúc nước đầy bể và ngừng bơm) được cho bởi hàm số $h’\left(t\right)=at+b$, với $a,b\in \mathbb{R}$. Lúc nước chảy hết ra ngoài thì tốc độ giảm chiều cao bằng 0 .

ĐỀ BÀI
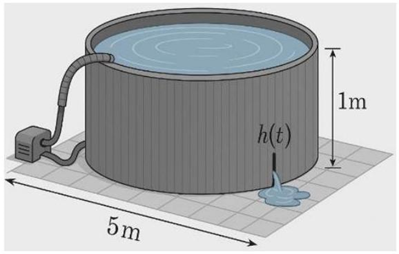
Một bể bơi hình trụ có đường kính 5 m và chiều cao 1 m ; bể được bơm nước vào với tốc độ không đổi $v_{0}$. Sau khi nước được bơm đầy, bể bơi bị thủng một lỗ ở đáy và nước chảy ra ngoài; bể bơi chảy hết nước trong 8 giờ. Biết tốc độ giảm chiều cao của bể bơi khi nước chảy ra ngoài vào thời điểm $t$ giờ (tính từ lúc nước đầy bể và ngừng bơm) được cho bởi hàm số $h’\left(t\right)=at+b$, với $a,b\in \mathbb{R}$. Lúc nước chảy hết ra ngoài thì tốc độ giảm chiều cao bằng 0 .

Lời giải
a) Thể tích của bể bơi sau khi nước được làm đầy là $6,25\pi \mathrm{\,\;}\mathrm{\,m}^{3}$.
b) $32a+1=0$ và $4b-1=0$.
c) Sau 4 giờ kể từ lúc bể bị rò, lượng nước bị mất đi bằng $\dfrac{75\pi }{16}\mathrm{\,\;}\mathrm{\,m}^{3}$.
d) Lượng nước bị rò rỉ ra ngoài một nửa sau $8-4\sqrt {2} $ giờ.
Lời giải:
a) Mệnh đề đúng.
Bể ước hình trụ có bán kính đáy $r=2,5\mathrm{\,\;m}$, chiều cao $h=1\mathrm{\,\;m}$
Thể tích khi đầy $V=\pi r^{2}h=\pi \cdot 2,5^{2}\cdot 1=6,25\pi \mathrm{\,\;}\mathrm{\,m}^{3}$.
b) Mệnh đề sai.
Ta có $h’\left(8\right)=0\Rightarrow 8a+b=0$ (1).
Chiều cao của nước thời điểm $t$ là $h\left(t\right)=\smallint \;\left(at+b\right)\mathrm{\,d}t=\dfrac{a}{2}t^{2}+bt+c$.
$\begin{array}{*{20}{c}}\mathrm{\,\;V\`i \;}\left\{\begin{array}{*{20}{l}}h\left(0\right)=1\\h\left(8\right)=0\end{array}\Rightarrow \left\{\begin{array}{*{20}{l}}c=1\\32a+8b+1=0\end{array}\right. \right. \# \left(2\right)\end{array}$
Từ (1) và (2) suy ra $a=\dfrac{1}{32},b=-\dfrac{1}{4}$. Khi đó $32a-1=0;4b+1=0$ và $h\left(t\right)=\dfrac{1}{64}t^{2}-\dfrac{1}{4}t+1$.
c) Mệnh đề đúng.
Chiều cao mực nước trong bể sau 4 giờ là: $h\left(4\right)=\dfrac{1}{64}\cdot 4^{2}-\dfrac{1}{4}\cdot 4+1=0,25\mathrm{\,\;m}$.
Lượng nước còn lại trong bể sau 4 giờ là $\pi r^{2}\cdot h\left(4\right)=\pi \cdot 2,5^{2}\cdot 0,25=\dfrac{25\pi }{16}m^{3}$.
Lượng nước đã thoát ra sau 4 giờ là $6,25\pi -\dfrac{25\pi }{16}=\dfrac{75\pi }{16}\mathrm{\,\;}\mathrm{\,m}^{3}$.
d) Mệnh đề đúng.
Lượng nước còn lại khi đã mất một nửa là $\dfrac{6,25\pi }{2}=\dfrac{25\pi }{8}\mathrm{\,\;}\mathrm{\,m}^{3}$.
Chiều cao tương ứng $h\left(t_{1}\right)$ của bể thỏa mãn $\pi \cdot 2,5^{2}\cdot h\left(t_{1}\right)=\dfrac{25\pi }{8}\Rightarrow h\left(t_{1}\right)=0,5\mathrm{\,\;m}$.
Ta có $h\left(t_{1}\right)=\dfrac{1}{64}t_{1}^{2}-\dfrac{1}{4}t_{1}+1=0,5\Rightarrow \left[\begin{array}{*{20}{l}}t_{1}=8+4\sqrt {2} \approx 13,7>8\\t_{1}=8-4\sqrt {2} \approx 2,3\in \left(0;8\right)\end{array}\right. $.
Ta thấy $t_{1}=8-4\sqrt {2} $ (giờ) thỏa mãn đề bài.