Thể tích khối đa diện

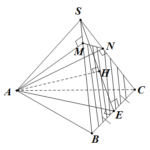
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh bằng $a. SA=2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $M,N$ tương ứng là hình chiếu vuông góc của $A$ trên $SB,SC$. Tìm thể tích khối chóp $A.BMNC$. Lời giải Ta có thể tích $V_{A.BMNC}=V_{S.ABC}-V_{S.AMN} (1)$Theo bài toán cơ bản thì $\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM}{SB}.\frac{SN}{SC}$Vì … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh bằng $a. SA=2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $M,N$ tương ứng là hình chiếu vuông góc của $A$ trên $SB,SC$. Tìm thể tích khối chóp $A.BMNC$.

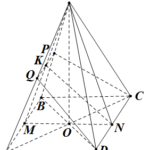
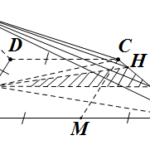
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$. Lời giải Gọi $M,N$ lần lượt là trung điểm $AB,CD. $ Khi đó $\widehat{SNM}=60^0$ là góc giữa … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$.

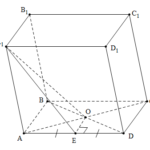
Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho. Lời giải Ta có $A_1O \bot (ABCD)$.Gọi $E$ là trung điểm … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho.

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a, AA'=2a, A'C=3a$. Gọi $M$ là trung điểm của $A'C'$ và $I$ là giao điểm của $AM$ và $A'C$. Tính thể tích tứ diện $IABC$. Lời giải Xét hệ tọa độ $Bxyz$ gốc $B$.Trong hệ trục tọa độ này ta có:$B=(0;0;0); A=(0;a;0); C=(2a;0;0)$(do … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a, AA'=2a, A'C=3a$. Gọi $M$ là trung điểm của $A'C'$ và $I$ là giao điểm của $AM$ và $A'C$. Tính thể tích tứ diện $IABC$.

Đề bài: Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, góc giữa hệ mặt phẳng $(A'BC), (ABC)$ bằng $60^0$. Tìm thể tích khối lăng trụ đó. Lời giải Gọi $M$ là trung điểm $BC$,ta có $AM \bot BC$     $A'M\bot BC$ (định lí ba đường vuông góc)Vậy $\widehat{A'MA}$ là góc tạo bởi hai mặt phẳng $(A'BC), (ABC)$ và $\widehat{A'MA}=60^0$Từ đó : … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, góc giữa hệ mặt phẳng $(A'BC), (ABC)$ bằng $60^0$. Tìm thể tích khối lăng trụ đó.

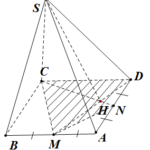
Đề bài: Cho hình chóp $S.ABCD $ đáy là hình vuông $ABCD$ cạnh $a$, mặt bên $SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Goi $M,N,P$ lần lượt là trung điểm $SB,BC,CD$. Tính thể tích tứ diện $CMNP$. Lời giải Gọi $H$ là trung điểm $AD$ thì $SH \bot AD$.Do $(SAD)\bot (ABCD)$ nên suy ra:  $SH \bot (ABCD); SH =\frac{a\sqrt{3}}{2}$ ( vì $ABC$ là … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD $ đáy là hình vuông $ABCD$ cạnh $a$, mặt bên $SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Goi $M,N,P$ lần lượt là trung điểm $SB,BC,CD$. Tính thể tích tứ diện $CMNP$.

Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A, D; AB=2AD=2a; CD=a$, góc giữa hai mặt phẳng $(SBC)$ và $(ABCD)$ bằng $60^0$ . Gọi $I$ là trung điểm của cạnh $AD$. Biết mặt phẳng $(SBI)$ và $(SCI)$cùng vuông góc với mặt phẳng $ABCD$. Tính thể tích khối chóp $S.ABCD$. Lời giải Vì $(SBI)$ và $(SCI)$ cùng vuông góc với đáy $ABCD$ nên giao tuyến $SI … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A, D; AB=2AD=2a; CD=a$, góc giữa hai mặt phẳng $(SBC)$ và $(ABCD)$ bằng $60^0$ . Gọi $I$ là trung điểm của cạnh $AD$. Biết mặt phẳng $(SBI)$ và $(SCI)$cùng vuông góc với mặt phẳng $ABCD$. Tính thể tích khối chóp $S.ABCD$.

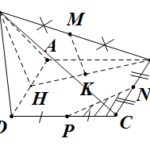
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Gọi $M, N$ lần lượt là trung điểm của $AB,AD$; $H$ là giao điểm của $CN \cap DM$. Biết $SH$ vuông góc với mặt phẳng $(ABCD)$ và $SH=a\sqrt{3}$. Tính thể tích khối chóp $S.CDNM$. Lời giải Ta có $V_{S.CDNM}=\frac{1}{3}SH. S_{CDNM}=\frac{1}{3}a\sqrt{3}.S_{CDNM}       (1)$.Lại có: … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Gọi $M, N$ lần lượt là trung điểm của $AB,AD$; $H$ là giao điểm của $CN \cap DM$. Biết $SH$ vuông góc với mặt phẳng $(ABCD)$ và $SH=a\sqrt{3}$. Tính thể tích khối chóp $S.CDNM$.