Đề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ đáy là hình vuông cạnh bằng $a$, chiều cao $AA'=b$. Gọi $M$ là trung điểm của cạnh $CC'$. Tính thể tích tứ diện $BDA'M$. Lời giải Trong $(ACC'A'): A'M \cap AC=E.$ Gọi $O$ là tâm của đáy $ABCD$ vì $M$ là trung điểm của $CC'$ , nên ta có $ CE=AC=a\sqrt{2}$Ta có: … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ đáy là hình vuông cạnh bằng $a$, chiều cao $AA'=b$. Gọi $M$ là trung điểm của cạnh $CC'$. Tính thể tích tứ diện $BDA'M$.
Thể tích khối đa diện
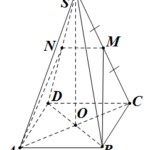
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$ Lời giải Normal 0 false … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$
Đề bài: Tính thể tích khôi tứ diện $ABCD$ biết $AB=a, AC=b,AD=c$ và các góc $\widehat{ABC},\widehat{CAD},\widehat{DAB}$ đều bằng $60^0$.
Đề bài: Tính thể tích khôi tứ diện $ABCD$ biết $AB=a, AC=b,AD=c$ và các góc $\widehat{ABC},\widehat{CAD},\widehat{DAB}$ đều bằng $60^0$. Lời giải cần giải chi tiết (đáp số $\frac{abc\sqrt{2}}{12})$. … [Đọc thêm...] vềĐề bài: Tính thể tích khôi tứ diện $ABCD$ biết $AB=a, AC=b,AD=c$ và các góc $\widehat{ABC},\widehat{CAD},\widehat{DAB}$ đều bằng $60^0$.
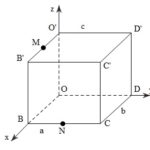
Đề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$
Đề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$ Lời giải a) Viết phương trình mặt phẳng $(\alpha )$ qua $M$ và song … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$
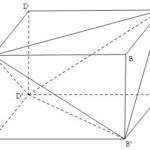
Đề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$
Đề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$ Lời giải Hình hộp chữ nhật có thể tích: $\begin{array}{l}V = abc\\{V_{{\rm{AA}}'B'D'}} = \frac{1}{6}abc\,\,\,;\,{V_{CC'D'B}} = \frac{1}{6}abc;\\{V_{BB'AC}} = \frac{1}{6}abc\,\,;\,\,{V_{{\rm{DD}}'AC}} = \frac{1}{6}abc\\ \Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$
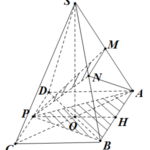
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$.
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$. Lời giải Do $MS=MA\Rightarrow d(A,(MNP))=d(S,(MNP)) (1) \Rightarrow V_{A.MNP}=V_{S.MNP}$Theo bài toán cơ bản, ta có:$\frac{V_{SMNP}}{V_{S.ABP}}=\frac{SM}{SA}.\frac{SN}{SB}=\frac{1}{4}\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$.
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$ Lời giải Cần giải chi tiết ( đáp số $\frac{2}{3}\frac{a^3}{\sqrt{a^2-16h^2}}$) … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$
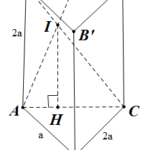
Đề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không?
Đề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không? Lời giải … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không?
Đề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$.
Đề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$. Lời giải Gọi $O$ là tâm của đáy $ABCD$. Trong tam giác $SAC$, ta có $NO$ là đường trung bình nên $NO // SA$, tức … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$.
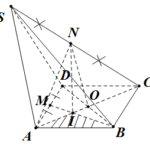
Đề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$.
Đề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$. Lời giải Trong tam giác vuông $A'AC$ ta có: $AC=\sqrt{9a^2-4a^2}=a\sqrt{5}$ Từ đó trong tam giác vuông $ABC$ thì : … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$.