Quan he song song

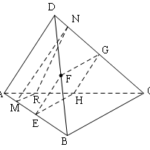
Đề bài: Cho tứ diện $ABCD$.Một điểm $M$ thuộc cạnh $AB$ và một điểm $N$ thuộc cạnh $CD$ sao cho : $\frac{AM}{AB}=\frac{DN}{DC}=k  $$a.$ Chứng minh ba đường thẳng $BC,MN,AD$ luôn song song với một mặt phẳng cố định khi $k$ thay đổi$b.$ Một điểm $P$ trên $BD$ và một điểm $Q$ trên $AC$ sao cho :$\frac{PD}{BD}=\frac{AQ}{AC}=k'    $Chứng minh rằng hai  đường thẳng $MN,PQ$ cắt … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$.Một điểm $M$ thuộc cạnh $AB$ và một điểm $N$ thuộc cạnh $CD$ sao cho : $\frac{AM}{AB}=\frac{DN}{DC}=k  $$a.$ Chứng minh ba đường thẳng $BC,MN,AD$ luôn song song với một mặt phẳng cố định khi $k$ thay đổi$b.$ Một điểm $P$ trên $BD$ và một điểm $Q$ trên $AC$ sao cho :$\frac{PD}{BD}=\frac{AQ}{AC}=k'    $Chứng minh rằng hai  đường thẳng $MN,PQ$ cắt nhau khi và chỉ khi $k=k'$

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó Lời giải Giao tuyến của mp $(MBC)$ và mp $(SAD)$ cắt $SD$ tại $N:MN//BC$ vì $AD//BC$$MB\bot BC$ vì $BC\bot … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó

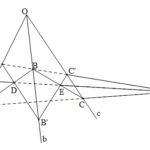
Đề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng. Lời giải Ta thấy, muốn chứng minh … [Đọc thêm...] vềĐề bài: Cho ba tia $Oa, Ob, Oc$ không cùng nằm trên một mặt phẳng; trên tia $Oa$ lấy $2$ điểm $A, A'$; trên tia $Ob$ lấy $2$ điểm $B, B'$; trên tia $Oc$ lấy $2$ điểm $C, C'$ sao cho $AB$ cắt $A'B'$ tại $D$, $BC$ cắt $B'C'$ tại $E$; $CA$ cắt $C'A'$ tại $G$. Chứng minh $D, E ,G$ thẳng hàng.

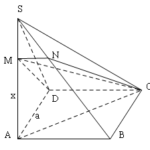
Đề bài: Cho chóp $S.ABCD$ có đáy $ABCD$  là hình vuông cạnh $a,SA\bot (ABCD);SA=a$. Mặt phẳng $(P)$ đi qua $CD$ cắt $SA,SB$ lần lượt tại $M,N$. Đặt $AM=x$. Tứ giác $MNCD$ là hình gì ? Tính diện tích tứ giác đó theo $a,x$ Lời giải Ta có : $DC//AB\Rightarrow  DC//(SAB)$$\Rightarrow  mp(MDC)\cap mp(SAB)=MN//AB$.Lại có $MN\bot (SAD)$.Suy ra tứ giác $MNCD$ là hình thang … [Đọc thêm...] vềĐề bài: Cho chóp $S.ABCD$ có đáy $ABCD$  là hình vuông cạnh $a,SA\bot (ABCD);SA=a$. Mặt phẳng $(P)$ đi qua $CD$ cắt $SA,SB$ lần lượt tại $M,N$. Đặt $AM=x$. Tứ giác $MNCD$ là hình gì ? Tính diện tích tứ giác đó theo $a,x$

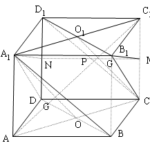
Đề bài: Cho hình hộp $ABCD.A_1B_1C_1D_1$$a.$ Chứng minh rằng $(BDA_1)//(B_1D_1C)$$b.$ Chứng minh đường chéo $AC_1$ đi qua các trọng tâm $G,G_1$ của $\Delta A_1BD$ và $\Delta CB_1D_1,G,G_1$ chia đoạn $AC_1$ làm $3$ phần bằng nhau.$c.$ Xác định thiết diện cắt bởi mặt phẳng $(A_1B_1G_1)$ với hình hộp đã cho. Thiết diện là hình gì ?$d.$ Gọi $O,K$ lần lượt là tâm các hình bình hành … [Đọc thêm...] vềĐề bài: Cho hình hộp $ABCD.A_1B_1C_1D_1$$a.$ Chứng minh rằng $(BDA_1)//(B_1D_1C)$$b.$ Chứng minh đường chéo $AC_1$ đi qua các trọng tâm $G,G_1$ của $\Delta A_1BD$ và $\Delta CB_1D_1,G,G_1$ chia đoạn $AC_1$ làm $3$ phần bằng nhau.$c.$ Xác định thiết diện cắt bởi mặt phẳng $(A_1B_1G_1)$ với hình hộp đã cho. Thiết diện là hình gì ?$d.$ Gọi $O,K$ lần lượt là tâm các hình bình hành $ABCD,BCC_1B_1$. Xác định thiết diện cắt bởi mặt phẳng $(A_1OK)$ với hình hộp đã cho

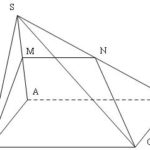
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình thang, đáy lớn $AB=3a,AD=CD=a$. Mặt bên $(SAB) $ là tam giác cân đỉnh $S$ với $SA=2a,\alpha$ là mặt phẳng di động song song với $(SAB)$ cắt các cạnh $AD,BC,SC,SD$ theo thứ tự tại $M,N,P,Q$$a.$ Chứng minh $MNPQ$ là hình thang cân$b.$ Đặt $x=AM$ với $0 Lời giải $a.$ Ta lần lượt có … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình thang, đáy lớn $AB=3a,AD=CD=a$. Mặt bên $(SAB) $ là tam giác cân đỉnh $S$ với $SA=2a,\alpha$ là mặt phẳng di động song song với $(SAB)$ cắt các cạnh $AD,BC,SC,SD$ theo thứ tự tại $M,N,P,Q$$a.$ Chứng minh $MNPQ$ là hình thang cân$b.$ Đặt $x=AM$ với $0

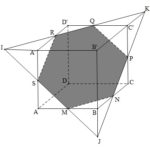
Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$  cắt hình lập phương. 

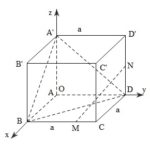
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $a$. Giả sử $M, N$ lần lượt là trung điểm của các cạnh $BC, DD'$a) Chứng minh rằng $MN//mp(A'BD)$B) Tính khoảng cách giữa hai đường thẳng $MN, BD$ Lời giải a) Chọn hệ trục tọa độ $Oxyz$ như sau:Gốc $O\equiv A$Trục $Ox$ đi qua $AB$Trục $Oy$ đi qua $AD$Trục $Oz$ đi qua $AA'$Khi đó … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $a$. Giả sử $M, N$ lần lượt là trung điểm của các cạnh $BC, DD'$a) Chứng minh rằng $MN//mp(A'BD)$B) Tính khoảng cách giữa hai đường thẳng $MN, BD$