Đề bài: Cho một mặt phẳng $(P)$ và một đường thẳng $b$ không nằm trong $(P)$ cắt $(P)$ tại một điểm $A.$ Chứng minh rằng mọi đường thẳng $a$ thuộc $(P)$ và không đi qua $A$ đều chéo nhau với $b$ Lời giải Nếu có một đường thẳng $a\in (P)$ mà không chéo với $b$ […]
Quan he song song
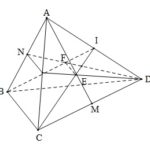
Đề bài: Cho tứ diện $ABCD$. $AM, DN$ theo thứ tự là các đường trung tuyến của các tam giác $ACD$ và $ABD$. $E\in AM, F\in DN$ sao cho $EF//BC$. Tìm tỉ số $\frac{EF}{BC}$.
Đề bài: Cho tứ diện $ABCD$. $AM, DN$ theo thứ tự là các đường trung tuyến của các tam giác $ACD$ và $ABD$. $E\in AM, F\in DN$ sao cho $EF//BC$. Tìm tỉ số $\frac{EF}{BC}$. Lời giải Ta có:Vì $EF//BC$ nên mp $BCEF$ cắt $AD$ tại $I$. Kẻ $NK//BC$ thì $K$ là trung điểm của $AC$. […]
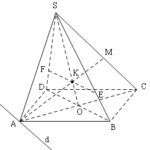
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình chữ nhật, có cạnh $AB=12cm,AD=5cm$.Mặt phẳng $(P)$ đi qua $A$ và một điểm $M$ thuộc cạnh $SC$ và song song với đường chéo $BD$$a.$ Chứng minh rằng khi $M$ di chuyển trên $SC$ thì mặt phẳng $(P)$ luôn đi qua một đường thẳng cố định.$b.$ Dựng giao tuyến của mặt phẳng $(P)$ với mặt phẳng $(SBD)$$c.$ Gọi các giao điểm của $mp(P)$ với $SB,SD$ theo thứ tự là $E,F$.Tính độ dài đoạn thẳng $EF$ khi điểm $M$ là trung điểm của đoạn thẳng $SC$
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình chữ nhật, có cạnh $AB=12cm,AD=5cm$.Mặt phẳng $(P)$ đi qua $A$ và một điểm $M$ thuộc cạnh $SC$ và song song với đường chéo $BD$$a.$ Chứng minh rằng khi $M$ di chuyển trên $SC$ thì mặt phẳng $(P)$ luôn đi qua một đường thẳng cố định.$b.$ […]
Đề bài: Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông, có $SA\bot (ABCD)$. Mặt phẳng $(\alpha)$ qua $A$ và song song $BD$ cắt $SC$ tại $N$, sao cho $SN=2NC$. Xác định thiết diện và chứng minh rằng thiết diện tạo thành là tứ giác có hai đường chéo vuông góc nhau
Đề bài: Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông, có $SA\bot (ABCD)$. Mặt phẳng $(\alpha)$ qua $A$ và song song $BD$ cắt $SC$ tại $N$, sao cho $SN=2NC$. Xác định thiết diện và chứng minh rằng thiết diện tạo thành là tứ giác có hai đường chéo vuông góc nhau Lời giải Để […]
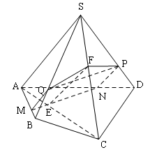
Đề bài: Cho hình chóp $S.ABCD$ và $M,N,Q$ là ba điểm lấy trên các cạnh $SA,SB,SD$$a.$ Xác định giao điểm $P$ của cạnh $SC$ với $mp(MNQ)$$b.$ Mặt phẳng $(MNQ)$ phải thỏa mãn điều kiện gì để tứ giác $MNPQ$ là hình thang?$c.$ Mặt phẳng $(MNQ)$ phải thỏa mãn điều kiện gì để tứ giác $MNPQ$ là hình bình hành?
Đề bài: Cho hình chóp $S.ABCD$ và $M,N,Q$ là ba điểm lấy trên các cạnh $SA,SB,SD$$a.$ Xác định giao điểm $P$ của cạnh $SC$ với $mp(MNQ)$$b.$ Mặt phẳng $(MNQ)$ phải thỏa mãn điều kiện gì để tứ giác $MNPQ$ là hình thang?$c.$ Mặt phẳng $(MNQ)$ phải thỏa mãn điều kiện gì để tứ giác $MNPQ$ […]
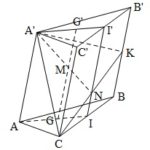
Đề bài: Cho lăng trụ tam giác $ABCA'B'C'$. $G$ và $G'$ là trọng tâm hai đáy. Qua trung điểm $M$ của $GG'$ kẻ một đường thẳng song song $CA'$, nó cắt mặt $ABB'A'$ và $BCC'A'$ tại $F, E$. Tìm độ dài $FE$ biết $CA'=a$.
Đề bài: Cho lăng trụ tam giác $ABCA'B'C'$. $G$ và $G'$ là trọng tâm hai đáy. Qua trung điểm $M$ của $GG'$ kẻ một đường thẳng song song $CA'$, nó cắt mặt $ABB'A'$ và $BCC'A'$ tại $F, E$. Tìm độ dài $FE$ biết $CA'=a$. Lời giải Kẻ các đường trung tuyến $AI$ và $A’I’$ […]
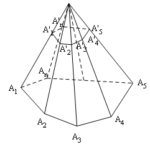
Đề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy.
Đề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy. Lời giải Giả sử hình chóp đã cho là $S.A_1A_2…A_n$; […]
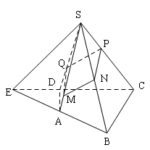
Đề bài: Cho hình chóp $S.ABCD$.Trên đoạn thẳng $AC$ lấy một điểm $E$ và trên cạnh $SC$ lấy mọt điểm $F$ sao cho :$\frac{AE}{AC} =\frac{SF}{SC} $Một mặt phẳng $(\alpha )$ đi qua đường thẳng $EF$ cắt các đường thẳng $AB,AD,SD,SB$ theo thứ tự tại các điểm $M,N,P,Q$$a.$ Chứng minh $MQ//NP$$b.$ Xác định vị trí các điểm $M,N$ để tứ giác $MNPQ$ là hình bình hành và thiết diện của hình chóp trong trường hợp này
Đề bài: Cho hình chóp $S.ABCD$.Trên đoạn thẳng $AC$ lấy một điểm $E$ và trên cạnh $SC$ lấy mọt điểm $F$ sao cho :$\frac{AE}{AC} =\frac{SF}{SC} $Một mặt phẳng $(\alpha )$ đi qua đường thẳng $EF$ cắt các đường thẳng $AB,AD,SD,SB$ theo thứ tự tại các điểm $M,N,P,Q$$a.$ Chứng minh $MQ//NP$$b.$ Xác định vị trí các […]
Đề bài: Cho hình chóp tứ giác $S.ABCD$.Gọi $E$ là giao điểm của hai đường thẳng $AB,CD$. Một mặt phẳng song song với đường thẳng $SE$ cắt các cạnh $SA,SB,SC$ theo thứ tự tại các điểm $M,N,P,Q$. Chứng minh $PQ//MN$
Đề bài: Cho hình chóp tứ giác $S.ABCD$.Gọi $E$ là giao điểm của hai đường thẳng $AB,CD$. Một mặt phẳng song song với đường thẳng $SE$ cắt các cạnh $SA,SB,SC$ theo thứ tự tại các điểm $M,N,P,Q$. Chứng minh $PQ//MN$ Lời giải Ta có : $SE//mp (\alpha )$$SE\subset (SAC)$$(\alpha )\cap (SAC)=PQ$$\Rightarrow PQ//SE (1)$Tương tự ta […]
Đề bài: Cho hai mặt phẳng $(P),(Q)$ giao nhau theo giao tuyến $\Delta $.Trong mặt phẳng $(P)$ lấy một điểm $A$ không thuộc $\Delta $ và trong mặt phẳng $(Q)$ lấy một điểm $B$ không thuộc $\Delta $.Chứng minh đường thẳng $AB$ và đường thẳng $\Delta $ là hai đường thẳng chéo nhau
Đề bài: Cho hai mặt phẳng $(P),(Q)$ giao nhau theo giao tuyến $\Delta $.Trong mặt phẳng $(P)$ lấy một điểm $A$ không thuộc $\Delta $ và trong mặt phẳng $(Q)$ lấy một điểm $B$ không thuộc $\Delta $.Chứng minh đường thẳng $AB$ và đường thẳng $\Delta $ là hai đường thẳng chéo nhau Lời giải […]