Đề bài: Cho hàm số $y = f(x) = mx^3 + 3mx^2-(m – 1)x – 1 $ với $m$ là tham số.$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $y = f(x)$ không có cực trị. […]
Khảo sát và vẽ đồ thị hàm số
Đề: Cho hàm số: $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2) Tìm k để đường thẳng $y = kx + 1$ cắt đồ thị $(C)$ tại hai điểm phân biệt $A, B$.3) Tìm quỹ tích trung điểm $I$ của đoạn $AB$ khi $k$ thay đổi
Đề bài: Cho hàm số: $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2) Tìm k để đường thẳng $y = kx + 1$ cắt đồ thị $(C)$ tại hai điểm phân biệt $A, B$.3) Tìm quỹ tích trung điểm […]
Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\).
Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\). Lời […]
Đề: a) Tùy theo các giá trị khác nhau của $m$, hãy lập bảng biến thiên của hàm số $y = \frac{{x + m}}{{\sqrt {{x^2} + 1} }}$b) Biện luận theo $m$ số nghiệm của phương trình $x + m = m\sqrt {{x^2} + 1} $
Đề bài: a) Tùy theo các giá trị khác nhau của $m$, hãy lập bảng biến thiên của hàm số $y = \frac{{x + m}}{{\sqrt {{x^2} + 1} }}$b) Biện luận theo $m$ số nghiệm của phương trình $x + m = m\sqrt {{x^2} + 1} $ Lời giải a) Hàm số xác […]
Đề: Cho hàm số $y=\frac{ax^2+3ax+2a+1}{x+2} $ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = – 1$.2) Chứng minh rằng tiệm cận xiên của (1) luôn đi qua một điểm cố định với mọi $a$.3) Với giá trị nào của $a$ thì đồ thị của (1) tiếp xúc với đường thẳng $y = a$
Đề bài: Cho hàm số $y=\frac{ax^2+3ax+2a+1}{x+2} $ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = – 1$.2) Chứng minh rằng tiệm cận xiên của (1) luôn đi qua một điểm cố định với mọi $a$.3) Với giá trị nào của $a$ thì đồ thị của (1) […]
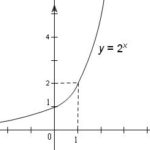
Đề: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$
Đề bài: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$ Lời giải $1)$.. Lập bảng biến thiên và vẽ đồ thị ($C$) của hàm số $y = {2^x}$ Đồ thị $({C^,})$của hàm số $y = {\left( {\frac{1}{2}} \right)^x}$ là đường […]
Đề: Cho hàm số $y = ax^3 + bx^2 + cx + d$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = c = 1;b = d = 0$.2) Giả sử $a > 0$. Chứng minh rằng trong số các tiếp tuyến của (1) thì tiếp tuyến tại điểm uốn sẽ có hệ số góc nhỏ nhất
Đề bài: Cho hàm số $y = ax^3 + bx^2 + cx + d$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = c = 1;b = d = 0$.2) Giả sử $a > 0$. Chứng minh rằng trong số các tiếp tuyến của (1) thì […]
Đề: Giải phương trình : ${2^{2{{\log }_3}\left( {{x^2} – 16} \right)}} + {2^{{{\log }_3}\left( {{x^2} – 16} \right) + 1}} = 24$
Đề bài: Giải phương trình : ${2^{2{{\log }_3}\left( {{x^2} – 16} \right)}} + {2^{{{\log }_3}\left( {{x^2} – 16} \right) + 1}} = 24$ Lời giải Đặt $t = {2^{{{\log }_3}\left( {{x^2} – 16} \right)}}$ $(x^{2}-16>0,t>0)$ Từ đề bài ta có : $t^{2}+2t-24=0$ $\Leftrightarrow t = 4 hoặc t=-6(loại)$ $t=4\Leftrightarrow \log_3(x^2-16)=2\Leftrightarrow x^2=25\Leftrightarrow x = \pm 5$Phương trình […]
Đề: Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số: $y = x + {e^{ – x}}$ Tính diện tích hình phẳng giớ hạn bởi ($C$) , đường tiệm cận xiên và các đường thẳng $x = 0,\,\,x = 1$
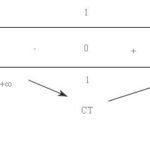
Đề bài: Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số: $y = x + {e^{ – x}}$ Tính diện tích hình phẳng giớ hạn bởi ($C$) , đường tiệm cận xiên và các đường thẳng $x = 0,\,\,x = 1$ Lời giải Tập xác định $R$. ${y^ / } […]
Đề: Cho hàm số:$y = \frac{x + 1}{x – 1}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.$2$. Chứng minh rằng mọi tiếp tuyến của đồ thị đều lập với hai đường tiệm cận một tam giác có diện tích không đổi.$3$. Tìm tất cả các điểm thuộc đồ thị sao cho tiếp tuyến tại đó lập với hai đường tiệm cận một tam giác có chu vi bé nhất.
Đề bài: Cho hàm số:$y = \frac{x + 1}{x – 1}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.$2$. Chứng minh rằng mọi tiếp tuyến của đồ thị đều lập với hai đường tiệm cận một tam giác có diện tích không đổi.$3$. Tìm tất cả các điểm thuộc đồ […]