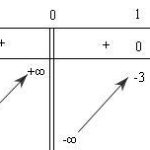
Đề bài: Cho hàm số : $y = (x - 1)(x^2 + mx + m)$ trong đó $m$ là tham số.$1.$ Khảo sát và vẽ đồ thị hàm của hàm số ứng với giá trị $m =-2.$$2.$ Tìm các giá trị của tham số m để đồ thị của hàm số tiếp xúc với trục hoành. Xác định tọa độ của tiếp điểm trong mỗi trường hợp tìm được. Lời giải $1.$ Bạn đọc tự giải$2.$ Hàm số $y' = ({x^2} + mx + m) + (x - 1)(2x + m)$Đồ thị hàm … [Đọc thêm...] vềĐề: Cho hàm số : $y = (x – 1)(x^2 + mx + m)$ trong đó $m$ là tham số.$1.$ Khảo sát và vẽ đồ thị hàm của hàm số ứng với giá trị $m =-2.$$2.$ Tìm các giá trị của tham số m để đồ thị của hàm số tiếp xúc với trục hoành. Xác định tọa độ của tiếp điểm trong mỗi trường hợp tìm được.
Khảo sát và vẽ đồ thị hàm số
Đề: Cho hàm số \(y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 1 – {m^2}\) có đồ thị \(\left( {{C_m}} \right)\) với $m$ là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi \(m = 2\)$2$. Tìm điều kiện của m để đồ thị \(\left( {{C_m}} \right)\) chứa hai điểm phân biệt, đối xứng nhau qua điểm $O(0, 0)$
Đề bài: Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 1 - {m^2}\) có đồ thị \(\left( {{C_m}} \right)\) với $m$ là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi \(m = 2\)$2$. Tìm điều kiện của m để đồ thị \(\left( {{C_m}} \right)\) chứa hai điểm phân biệt, đối xứng nhau qua điểm $O(0, 0)$ Lời giải $1$. Bạn đọc tự giải$2$. \(\left( {{C_m}} … [Đọc thêm...] vềĐề: Cho hàm số \(y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 1 – {m^2}\) có đồ thị \(\left( {{C_m}} \right)\) với $m$ là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi \(m = 2\)$2$. Tìm điều kiện của m để đồ thị \(\left( {{C_m}} \right)\) chứa hai điểm phân biệt, đối xứng nhau qua điểm $O(0, 0)$
Đề: Cho hàm số: $f(x) = x^n + (c – n)^n$. Trong đó $c > 0$, và $n$ là một số nguyên dương lớn hơn $1$.a) Khảo sát sự biến thiên của hàm số đó.b) Từ kết quả ấy, chứng minh bất đẳng thức: ${( {\frac{{a + b}}{2}} )^n} \le \frac{{{a^n} + {b^n}}}{2}$Với $a, b$ là hai số tùy ý thỏa mãn điều kiện $a + b \ge 0$ còn $n$ là số nguyên dương bất kỳ
Đề bài: Cho hàm số: $f(x) = x^n + (c - n)^n$. Trong đó $c > 0$, và $n$ là một số nguyên dương lớn hơn $1$.a) Khảo sát sự biến thiên của hàm số đó.b) Từ kết quả ấy, chứng minh bất đẳng thức: ${( {\frac{{a + b}}{2}} )^n} \le \frac{{{a^n} + {b^n}}}{2}$Với $a, b$ là hai số tùy ý thỏa mãn điều kiện $a + b \ge 0$ còn $n$ là số nguyên dương bất kỳ Lời giải a) Hàm số được xác … [Đọc thêm...] vềĐề: Cho hàm số: $f(x) = x^n + (c – n)^n$. Trong đó $c > 0$, và $n$ là một số nguyên dương lớn hơn $1$.a) Khảo sát sự biến thiên của hàm số đó.b) Từ kết quả ấy, chứng minh bất đẳng thức: ${( {\frac{{a + b}}{2}} )^n} \le \frac{{{a^n} + {b^n}}}{2}$Với $a, b$ là hai số tùy ý thỏa mãn điều kiện $a + b \ge 0$ còn $n$ là số nguyên dương bất kỳ
Đề: Cho hàm số $y = f(x) = x^3 + ax + 2$ với $a$ là tham số.$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a =-3.$$2$. Tìm tất cả các giá trị của $a$ để đồ thị hàm số $y = f(x)$ cắt trục hoành tại một và chỉ một điểm.
Đề bài: Cho hàm số $y = f(x) = x^3 + ax + 2$ với $a$ là tham số.$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a =-3.$$2$. Tìm tất cả các giá trị của $a$ để đồ thị hàm số $y = f(x)$ cắt trục hoành tại một và chỉ một điểm. Lời giải $1$). Xin dành cho bạn đọc.$2$). Hoành độ giao điểm với trục hoành là nghiệm phương trình $x^3{\rm{ + ax + 2 = 0}} … [Đọc thêm...] vềĐề: Cho hàm số $y = f(x) = x^3 + ax + 2$ với $a$ là tham số.$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a =-3.$$2$. Tìm tất cả các giá trị của $a$ để đồ thị hàm số $y = f(x)$ cắt trục hoành tại một và chỉ một điểm.
Đề: Cho hàm số: $y = \frac{3(x + 1)}{x – 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên.
Đề bài: Cho hàm số: $y = \frac{3(x + 1)}{x - 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên. Lời giải $1.$ Bạn đọc tự giải$2.$ Phương trình tiếp tuyến tại điểm $M_0(x_0,y_0)\in (C)$ là$y=-\frac{9}{(x_0-2)^2}(x-x_0)+y_0 … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{3(x + 1)}{x – 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên.
Đề: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$.
Đề bài: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$. Lời giải $1$. \(y' = \frac{{{x^2} + 2x + 1 - m}}{{{{\left( {x + 1} \right)}^2}}}\) Đồ thị có các điểm cực đại, cực … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$.
Đề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$
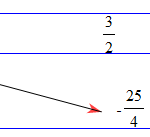
Đề bài: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$ Lời giải Giải* Tập xác định $R$* Sự biến thiên: Ta có: $a=1>0, -\frac{b}{2a}=\frac{3}{2}, -\frac{\Delta}{4a}=-\frac{25}{4}$. Vậy đồ thị hàm số $y=x^2-3x-4$ là parabol có đỉnh $I(\frac{3}{2};-\frac{25}{4})$, nhận đường thẳng $x=\frac{3}{2}$ làm tâm đối xứng và bề lõm hướng lên trên. Suy ra: Hàm số nghịch biến trên khoảng … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$
Đề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề bài: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x - 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau Lời giải $1$. Bạn đọc tự giải$2$. Xét \(A\left( {0,a} \right)\) trên $Oy$. Đường thẳng qua $A$ với hệ số góc $k$ có phương trình \(y = kx + … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề bài: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y - x + 6 = 0$ Lời giải $1)$ Viết lại biểu … [Đọc thêm...] vềĐề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)
Đề bài: Cho hàm số \(y = \frac{{{x^2} - x - 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} - \left( {1 + m} \right)|x| - m - 1 = 0\) Lời … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)