Một chiếc container được buộc vào móc S của một chiếc cần cẩu bởi bốn sợi dây cáp không giãn $SA, SB, SC, SD$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $45^{\circ}$ (tham khảo hình vẽ bên dưới)

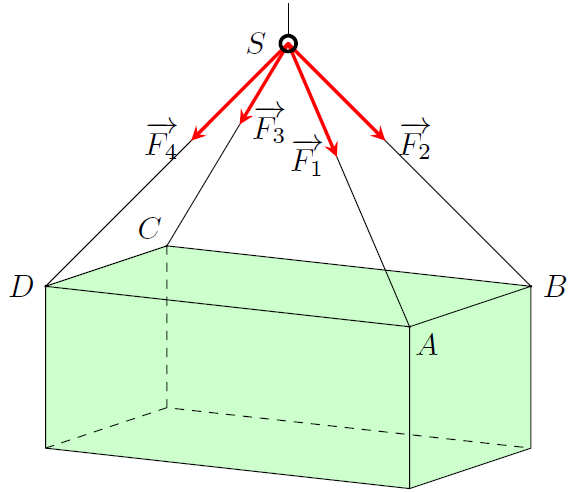
Một chiếc container được buộc vào móc S của một chiếc cần cẩu bởi bốn sợi dây cáp không giãn $SA, SB, SC, SD$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $45^{\circ}$ (tham khảo hình vẽ bên dưới). Chiếc cần cẩu kéo chiếc container lên theo phương thẳng đứng. Tính cường độ lực căng (đơn vị kN) của mỗi sợi dây cáp (làm tròn kết quả đến chữ số hàng phần chục), biết rằng các lực căng ${{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},{{\overrightarrow{F}}_{3}},{{\overrightarrow{F}}_{4}}$ trên mỗi sợi dây cáp đều có cường độ bằng nhau và trọng lượng của chiếc container bằng 68 kN. (Kết quả làm tròn đến 1 chữ số sau dấu phẩy).

Đáp án: 24
Lời giải: Để đơn giản ta đồng nhất ${{\vec{F}}_{1}}=\overrightarrow{SA},{{\vec{F}}_{2}}=\overrightarrow{SB},{{\vec{F}}_{3}}=\overrightarrow{SC},{{\vec{F}}_{4}}=\overrightarrow{SD}$. Gọi $O=AB\cap BD$.
Khi đó $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\left( \overrightarrow{SA}+\overrightarrow{SC} \right)+\left( \overrightarrow{SB}+\overrightarrow{SD} \right)=2\overrightarrow{SO}+2\overrightarrow{SO}=4\overrightarrow{SO}$
Suy ra $4SO=68\Rightarrow SO=17$
$\sin {{45}^{\circ}}=\dfrac{SO}{SA}\Rightarrow SA=\dfrac{SO}{\sin {{45}^{\circ}}}\approx 24,0416$