
====
Câu hỏi:
Trong không gian với hệ trục tọa độ Oxyz, cho ba đường thẳng\({d_1}:\left\{ \begin{array}{l}x = 1\\y = – 1\\z = {t_1}\end{array} \right.,{d_2}:\left\{ \begin{array}{l}x = {t_2}\\y = – 1\\z = 0\end{array} \right.,{d_3}:\left\{ \begin{array}{l}x = 1\\y = {t_3}\\z = 0\end{array} \right..\) Viết phương trình mặt phẳng đi qua M(1;2;3) và cắt ba đường thẳng \({d_1},{d_2},{d_3}\)lần lượt tại A, B, C sao cho M là trực tâm tam giác ABC.
- A. \(y + z – 5 = 0\)
- B. \(x – z – 2 = 0\)
- C. \(2x + 2y – z – 9 = 0\)
- D. \(x + y + z – 6 = 0\)
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: A
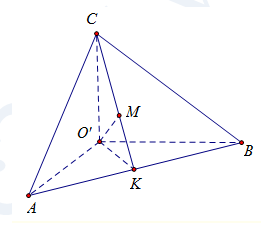
Dễ thấy \({d_1};{d_2};{d_3}\)đôi một vuông góc và đồng quy tại điểm
O’(1;-1;0).
Gọi M là trực tâm tam giác ABC.
Khi đó \(\left\{ \begin{array}{l}CM \bot AB\\O’C \bot AB\end{array} \right. \Rightarrow AB \bot O’M\),
tương tự \(BC \bot O’M\)
Suy ra \(O’M \bot \left( {ABC} \right)\). Lại có \(\overrightarrow {O’M} = \left( {0;3;3} \right)\)
Khi đó \(\left( {ABC} \right)\) qua \(M\left( {1;2;3} \right)\) và nhận \(\overrightarrow {OM} \)và VTPT có phương trình là \(y + z – 5 = 0.\)
=======|+|
Xem lại lý thuyết Phương pháp tọa độ trong không gian
