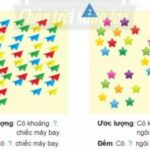
Giải bài tập SGK Toán 2 - tập 1 - Sách Chân trời sáng tạo - Giải toán 2 tập 1 bài: Ước lượng ============ Giải toán 2 tập 1 bài: Ước lượng Chương 1. ÔN TẬP VÀ BỔ SUNG - (CTST) ============= 1. Ước lượng rồi đếm Hướng dẫn: 1. Ước lượng rồi đếm Hướng dẫn: 2. Ước lượng rồi đếm Hướng dẫn: 3. Ước lượng rồi đếm Hướng dẫn: ====== 1. ÔN TẬP VÀ BỔ SUNG - … [Đọc thêm...] vềGiải toán 2 tập 1 bài: Ước lượng – Toán lớp 2 – Sách Chân trời sáng tạo
Giải toán 2 tập 1 bài: Ôn tập các số đến 100 – Toán lớp 2 – Sách Chân trời sáng tạo
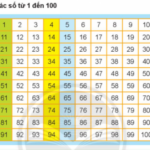
Giải bài tập SGK Toán 2 - tập 1 - Sách Chân trời sáng tạo - Giải toán 2 tập 1 bài: Ôn tập các số đến 100 ============ Giải toán 2 tập 1 bài: Ôn tập các số đến 100 Chương 1. ÔN TẬP VÀ BỔ SUNG - (CTST) ============= 1. Đọc số: a. Đọc các số theo thứ tự từ 1 đến 100 và ngược lại b. Đọc các số tròn chục: 10, 20,...., 100 c. Đọc các số cách 5 đơn vị : … [Đọc thêm...] vềGiải toán 2 tập 1 bài: Ôn tập các số đến 100 – Toán lớp 2 – Sách Chân trời sáng tạo
Trong không gian với hệ trục tọa độ \(Oxyz\), cho 2 đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y – 1}}{{ – 1}} = \frac{{z – 2}}{1}\) và \({d_2}:\frac{{x + 2}}{1} = \frac{y}{1} = \frac{{z + 1}}{{ – 1}}\). Đường thẳng vuông góc với mặt phẳng \(\left( {Oxy} \right)\) và cắt \({d_1},{d_2}\) có phương trình là
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian với hệ trục tọa độ \(Oxyz\), cho 2 đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 2}}{1}\) và \({d_2}:\frac{{x + 2}}{1} = \frac{y}{1} = \frac{{z + 1}}{{ - … [Đọc thêm...] vềTrong không gian với hệ trục tọa độ \(Oxyz\), cho 2 đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y – 1}}{{ – 1}} = \frac{{z – 2}}{1}\) và \({d_2}:\frac{{x + 2}}{1} = \frac{y}{1} = \frac{{z + 1}}{{ – 1}}\). Đường thẳng vuông góc với mặt phẳng \(\left( {Oxy} \right)\) và cắt \({d_1},{d_2}\) có phương trình là
Trong không gian với hệ toạ độ \(Oxyz\), cho hai đường thẳng \({d_1}:\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ – 1}}\) và\({d_2}:\frac{{x – 1}}{1} = \frac{{y + 2}}{3} = \frac{{z – 2}}{{ – 2}}\). Gọi \(\Delta \) là đường thẳng song song với \(\left( P \right):x + y + z – 7 = 0\) và cắt \({d_1},{\rm{ }}{d_2}\) lần lượt tại hai điểm \(A,B\) sao cho\(AB\) ngắn nhất. Phương trình của đường thẳng \(\Delta \) là
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian với hệ toạ độ \(Oxyz\), cho hai đường thẳng \({d_1}:\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ - 1}}\) và\({d_2}:\frac{{x - 1}}{1} = \frac{{y + 2}}{3} = \frac{{z - 2}}{{ - … [Đọc thêm...] vềTrong không gian với hệ toạ độ \(Oxyz\), cho hai đường thẳng \({d_1}:\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ – 1}}\) và\({d_2}:\frac{{x – 1}}{1} = \frac{{y + 2}}{3} = \frac{{z – 2}}{{ – 2}}\). Gọi \(\Delta \) là đường thẳng song song với \(\left( P \right):x + y + z – 7 = 0\) và cắt \({d_1},{\rm{ }}{d_2}\) lần lượt tại hai điểm \(A,B\) sao cho\(AB\) ngắn nhất. Phương trình của đường thẳng \(\Delta \) là
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x + 2}}{4} = \frac{{y – 1}}{{ – 4}} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):2x – y + 2z + 1 = 0\). Đường thẳng \(\Delta \) đi qua \(E\left( { – 2\,;\,\,1\,;\, – 2} \right)\), song song với \(\left( P \right)\) đồng thời tạo với \(d\) góc bé nhất. Biết rằng \(\Delta \) có một vectơ chỉ phương \(\vec u = \left( {m\,;\,n\,;\,1} \right).\) Tính \(T = {m^2} – {n^2}\).
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x + 2}}{4} = \frac{{y - 1}}{{ - 4}} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):2x - y + 2z + 1 = 0\). Đường thẳng \(\Delta \) đi qua … [Đọc thêm...] vềTrong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x + 2}}{4} = \frac{{y – 1}}{{ – 4}} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):2x – y + 2z + 1 = 0\). Đường thẳng \(\Delta \) đi qua \(E\left( { – 2\,;\,\,1\,;\, – 2} \right)\), song song với \(\left( P \right)\) đồng thời tạo với \(d\) góc bé nhất. Biết rằng \(\Delta \) có một vectơ chỉ phương \(\vec u = \left( {m\,;\,n\,;\,1} \right).\) Tính \(T = {m^2} – {n^2}\).
Trong không gian \(Oxyz\), cho đường thằng \(\Delta :\left\{ \begin{array}{l}x = 3t + 1\\y = t\\z = 2t – 1\end{array} \right.\) và 2 đường thẳng \({d_1}:\frac{{x + 2}}{{ – 1}} = \frac{y}{2} = \frac{{x – 1}}{2}\), \({d_2}:\frac{{x – 3}}{2} = \frac{{y – 1}}{1} = \frac{z}{1}\). Đường thẳng \(d’\) song song \(\Delta \), đồng thời cắt cả \({d_1}\), \({d_2}\) có phương trình là
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian \(Oxyz\), cho đường thằng \(\Delta :\left\{ \begin{array}{l}x = 3t + 1\\y = t\\z = 2t - 1\end{array} \right.\) và 2 đường thẳng \({d_1}:\frac{{x + 2}}{{ - 1}} = \frac{y}{2} = \frac{{x - … [Đọc thêm...] vềTrong không gian \(Oxyz\), cho đường thằng \(\Delta :\left\{ \begin{array}{l}x = 3t + 1\\y = t\\z = 2t – 1\end{array} \right.\) và 2 đường thẳng \({d_1}:\frac{{x + 2}}{{ – 1}} = \frac{y}{2} = \frac{{x – 1}}{2}\), \({d_2}:\frac{{x – 3}}{2} = \frac{{y – 1}}{1} = \frac{z}{1}\). Đường thẳng \(d’\) song song \(\Delta \), đồng thời cắt cả \({d_1}\), \({d_2}\) có phương trình là
Trong không gian hệ tọa độ \(Oxyz\), cho 4 đường thẳng \({d_1}:\frac{{x – 1}}{1} = \frac{{y – 6}}{{ – 2}} = \frac{{z – 5}}{1}\), \({d_2}:\frac{{x + 2}}{3} = \frac{{y – 4}}{{ – 6}} = \frac{{z – 7}}{3}\), \({d_3}:\frac{{x – 1}}{4} = \frac{{y + 2}}{{ – 4}} = \frac{{z – 1}}{{ – 3}}\), \({d_4}:\frac{{x + 13}}{{13}} = \frac{{y – 4}}{{13}} = \frac{{z – 13}}{{ – 13}}\). Gọi \(d\) là đường thẳng cắt cả 4 đường thẳng trên. Điểm nào sau đây thuộc \(d\)?
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian hệ tọa độ \(Oxyz\), cho 4 đường thẳng \({d_1}:\frac{{x - 1}}{1} = \frac{{y - 6}}{{ - 2}} = \frac{{z - 5}}{1}\), \({d_2}:\frac{{x + 2}}{3} = \frac{{y - 4}}{{ - 6}} = \frac{{z - 7}}{3}\), … [Đọc thêm...] vềTrong không gian hệ tọa độ \(Oxyz\), cho 4 đường thẳng \({d_1}:\frac{{x – 1}}{1} = \frac{{y – 6}}{{ – 2}} = \frac{{z – 5}}{1}\), \({d_2}:\frac{{x + 2}}{3} = \frac{{y – 4}}{{ – 6}} = \frac{{z – 7}}{3}\), \({d_3}:\frac{{x – 1}}{4} = \frac{{y + 2}}{{ – 4}} = \frac{{z – 1}}{{ – 3}}\), \({d_4}:\frac{{x + 13}}{{13}} = \frac{{y – 4}}{{13}} = \frac{{z – 13}}{{ – 13}}\). Gọi \(d\) là đường thẳng cắt cả 4 đường thẳng trên. Điểm nào sau đây thuộc \(d\)?
Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):3x – 5y + 2z + 8 = 0\) và đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 7 + 5t}\\{y = – 7 + t}\\{z = 6 – 5t}\end{array}} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\). Tìm phương trình đường thẳng \(\Delta \) đối xứng với đường thẳng \(d\) qua mặt phẳng \(\left( P \right).\)
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):3x - 5y + 2z + 8 = 0\) và đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 7 + 5t}\\{y = - 7 + t}\\{z = 6 - 5t}\end{array}} … [Đọc thêm...] vềTrong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):3x – 5y + 2z + 8 = 0\) và đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 7 + 5t}\\{y = – 7 + t}\\{z = 6 – 5t}\end{array}} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\). Tìm phương trình đường thẳng \(\Delta \) đối xứng với đường thẳng \(d\) qua mặt phẳng \(\left( P \right).\)
Phương trình đường thẳng song song với đường thẳng \(d:\frac{{x – 1}}{1} = \frac{{y + 2}}{1} = \frac{z}{{ – 1}}\) và cắt hai đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y + 1}}{1} = \frac{{z – 2}}{{ – 1}}\); \({d_2}:\frac{{x – 1}}{{ – 1}} = \frac{{y – 2}}{1} = \frac{{z – 3}}{3}\) là
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Phương trình đường thẳng song song với đường thẳng \(d:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{z}{{ - 1}}\) và cắt hai đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y + 1}}{1} = \frac{{z - 2}}{{ … [Đọc thêm...] vềPhương trình đường thẳng song song với đường thẳng \(d:\frac{{x – 1}}{1} = \frac{{y + 2}}{1} = \frac{z}{{ – 1}}\) và cắt hai đường thẳng \({d_1}:\frac{{x + 1}}{2} = \frac{{y + 1}}{1} = \frac{{z – 2}}{{ – 1}}\); \({d_2}:\frac{{x – 1}}{{ – 1}} = \frac{{y – 2}}{1} = \frac{{z – 3}}{3}\) là
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;1;3} \right),M\left( { – 2;1;0} \right)\) và mặt phẳng \(\left( \alpha \right):x – y + 2 = 0\). Viết phương trình mặt phẳng đi qua hai điểm \(A,M\) và cắt \(\left( \alpha \right)\) theo một giao tuyến vuông góc với \(AM\).
DẠNG TOÁN 45: DẠNG 45 PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN ĐIỀU KIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;1;3} \right),M\left( { - 2;1;0} \right)\) và mặt phẳng \(\left( \alpha \right):x - y + 2 = 0\). Viết phương trình mặt phẳng đi qua hai … [Đọc thêm...] vềTrong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;1;3} \right),M\left( { – 2;1;0} \right)\) và mặt phẳng \(\left( \alpha \right):x – y + 2 = 0\). Viết phương trình mặt phẳng đi qua hai điểm \(A,M\) và cắt \(\left( \alpha \right)\) theo một giao tuyến vuông góc với \(AM\).