Ở một sân bay, vị trí của máy bay được xác định bởi điểm ${M}$ trong không gian ${Oxyz}$ như hình vẽ

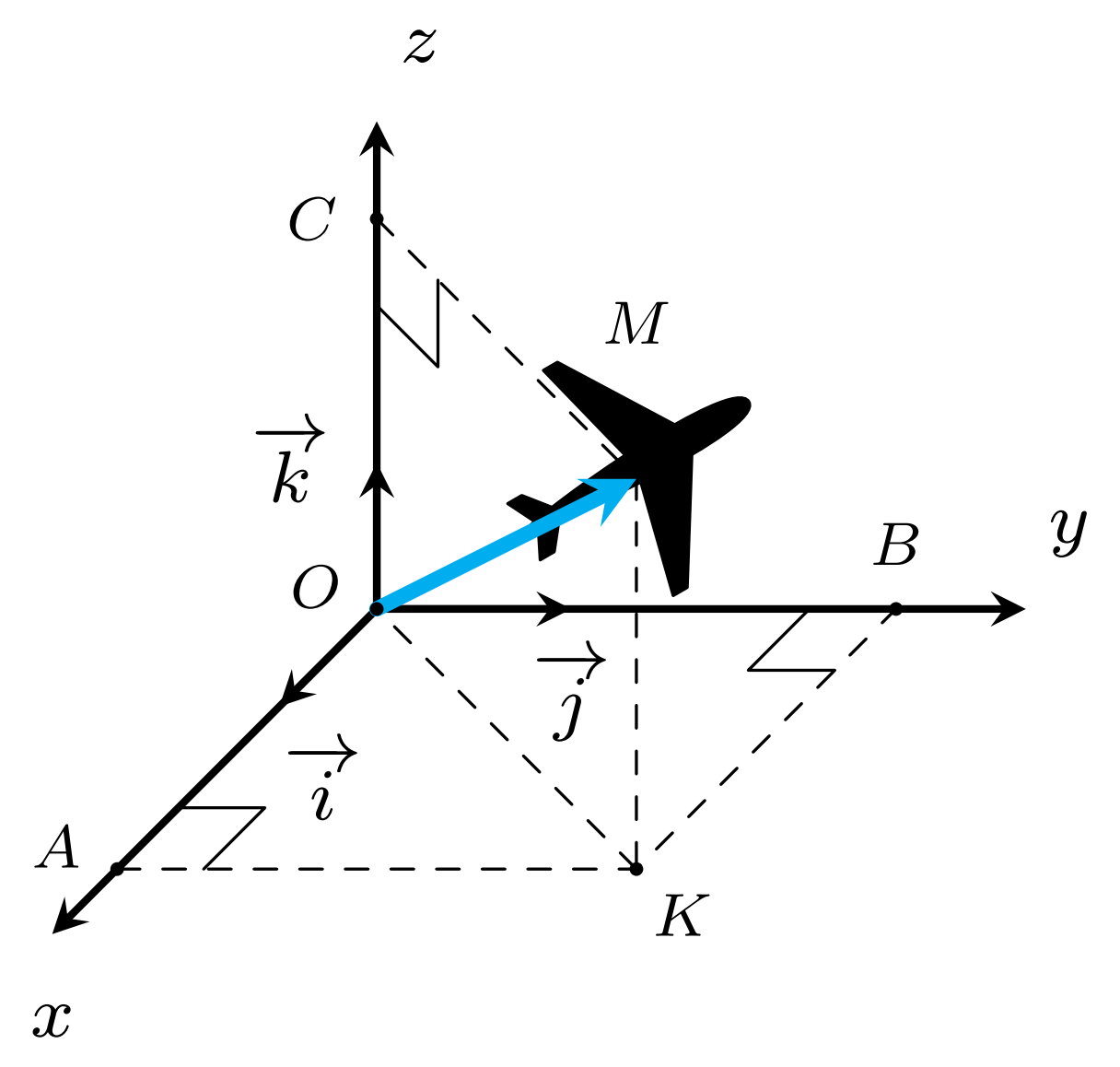
Ở một sân bay, vị trí của máy bay được xác định bởi điểm ${M}$ trong không gian ${Oxyz}$ như hình vẽ. Gọi ${K}$ là hình chiếu vuông góc của ${M}(a;b;c)$ xuống mặt phẳng $(Oxy)$.
Cho biết $OM = 47$, $\left(\overrightarrow{i},\overrightarrow{OK}\right) = 65^\circ$, $\left(\overrightarrow{OK},\overrightarrow{OM}\right) = 57^\circ$. Tính $a+b+c$ (làm tròn đến hàng đơn vị).

Đáp án: 73
Lời giải: Ta có: $OK=OM\cos 57^\circ=25,60$
$OC=OM\sin 57^\circ=39,42$
$OA=OK\cos 65^\circ=10,82$
$OB=AK=OK\sin 65^\circ=23,20$
$\Rightarrow M(10,82;23,20;39,42)\Rightarrow a+b+c=73,0$.