Hình vẽ dưới đây mô tả một sân cầu lông với kích thước theo tiêu chuẩn quốc tế

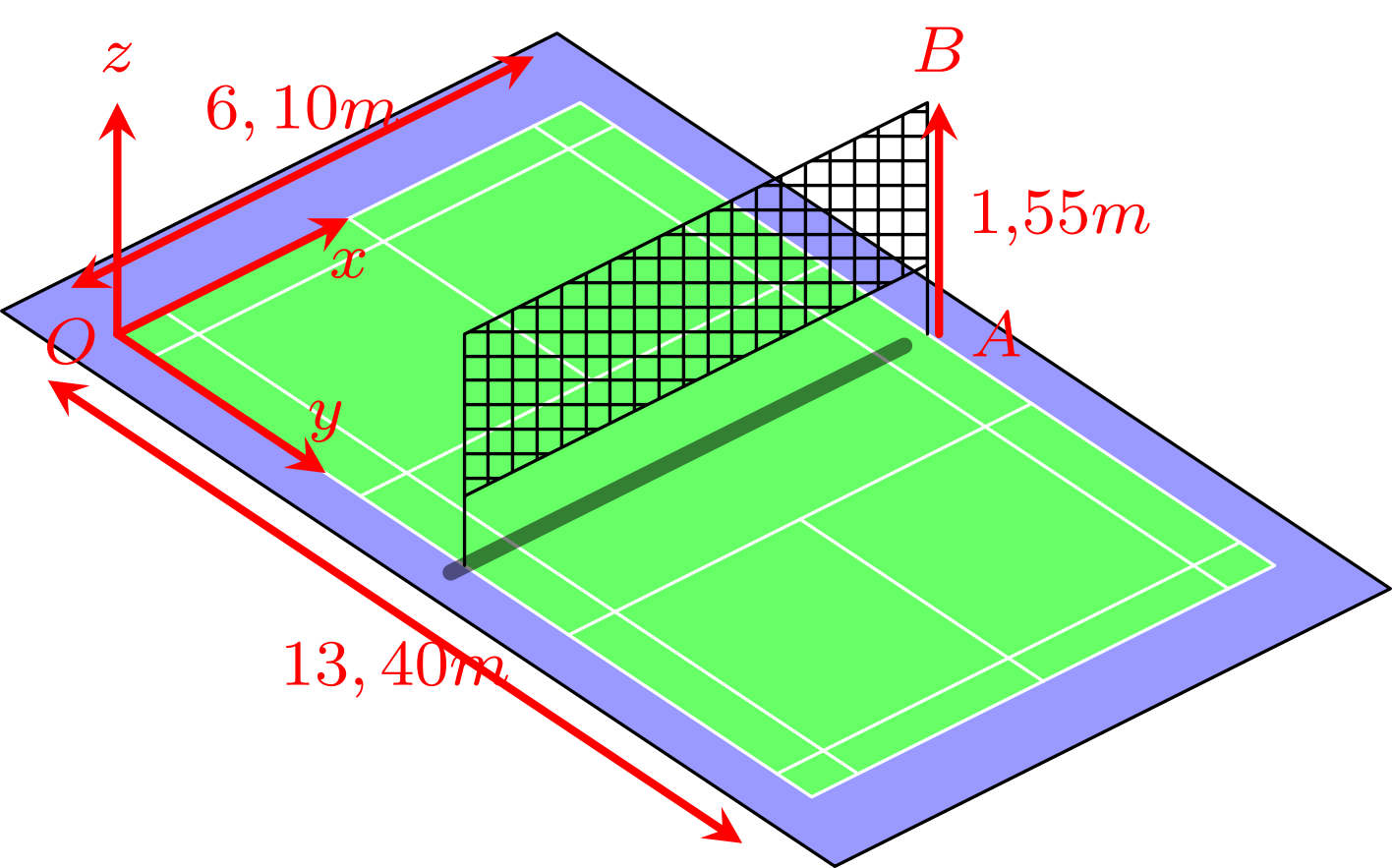
Hình vẽ dưới đây mô tả một sân cầu lông với kích thước theo tiêu chuẩn quốc tế. Ta chọn hệ trục $Oxyz$ cho sân đó như hình vẽ (đơn vị trên mỗi trục là mét). Giả sử $AB$ là một trụ cầu lông để căng lưới. Gọi $(x;y;z)$ là tọa độ của vectơ $\overrightarrow{AB}$. Tính $x+y+z$.

Đáp án: 1,55
Lời giải: $\bullet$ Gọi toạ độ điểm $A$ là $\left(x_A;y_A;z_A\right)$. Vì chiều rộng của sân là $6,1 \mathrm{~m}$ nên $x_A=6,1$. Do một nửa chiều dài của sân là $6,7 \mathrm{~m}$ nên $y_A=6,7$. Điểm $A$ thuộc mặt phẳng $(Oxy)$ nên $z_A=0$. Vì vậy, điểm $A$ có tọa độ là $(6,1;6,7;0)$.
$\bullet$ Độ dài đoạn thẳng $AB$ là $1,55 \mathrm{~m}$ nên điểm $B$ có toạ độ là $(6,1;6,7;1,55)$.
Vậy ta có $\overrightarrow{AB}=(6,1-6,1;6,7-6,7;1,55-0)$, tức là $\overrightarrow{AB}=(0;0;1,55)$.
Vậy $x+y+z=1{,}55$.