Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $20$ cm.
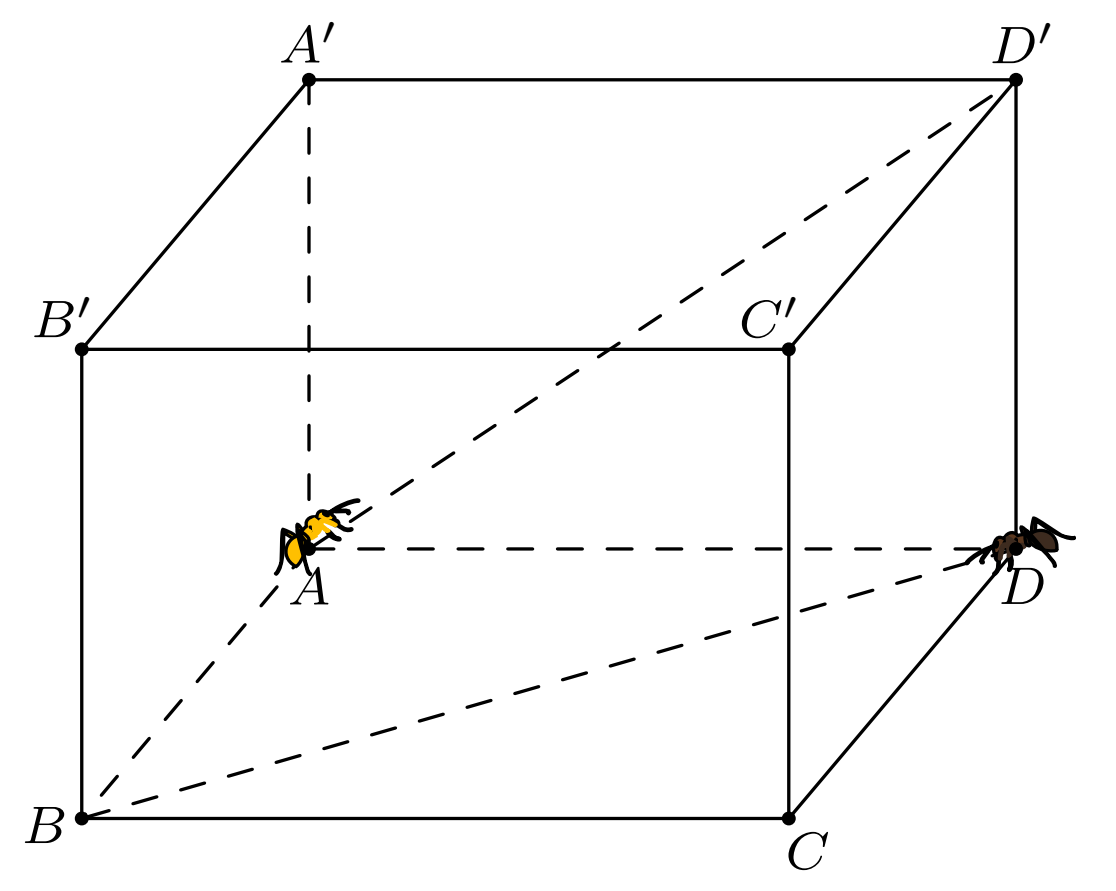
Hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí $A$ và $D$, kiến vàng đi từ $A$ đến $D’$ với vận tốc $2\text{cm/s}$ và kiến đen đi từ $D$ đến $B$ với vận tốc $3\text{cm/s}$. Hỏi khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu $\text{cm}$? (Viết kết quả làm tròn đến hàng phần chục).
Đáp án: 19,3
Lời giải:
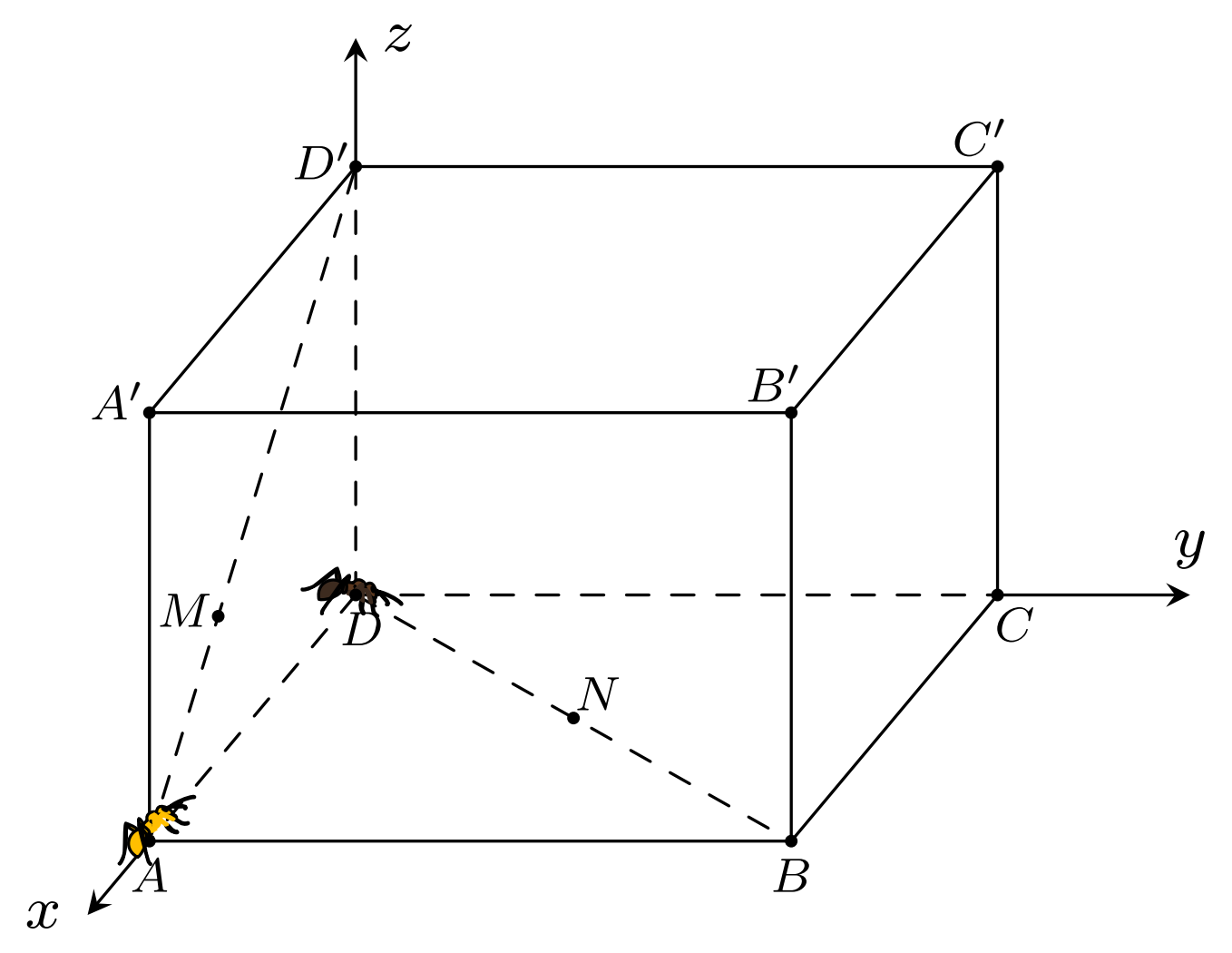
Giả sử trong khoảng thời gian $x$ (s) ($x{>}0$) kiến vàng đi được quãng đường là $AM=2x$ cm, khi đó kiến đen đi được quãng đường là $DN=3x$, cm.
Không mất tính tổng quát, ta giả sử rằng hình lập phương có độ dài cạnh bằng $1$ cm và ta đặt hệ trục tọa độ $Dxyz$ như hình vẽ trên.
Từ đó suy ra $AD’=DB=\sqrt{2}$ cm; $D=(0;0;0)$, $B=(1;1;0)$, $A(1,0,0)$ và $D'(0;0,1)$.
Suy ra $\overrightarrow{AD’}=(1;0;-1)$, $\overrightarrow{DB}=(1;1;0)$; $\overrightarrow{AM}=(x_M-1;y_M,z_M)$; $\overrightarrow{DN}=(x_N;y_N,z_N)$.
Ta có $\left\{\begin{array}{l} \overrightarrow{AM}=\dfrac{2x}{AD’}\overrightarrow{AD’}=\dfrac{2x}{\sqrt{2}}\overrightarrow{AD’}=\left(\dfrac{2x}{\sqrt{2}};0;-\dfrac{2x}{\sqrt{2}}\right)\\ \overrightarrow{DN}=\dfrac{3x}{DB}\overrightarrow{DB}=\dfrac{3x}{\sqrt{2}}\overrightarrow{DB}=\left(\dfrac{3x}{\sqrt{2}};\dfrac{3x}{\sqrt{2}};0\right) \end{array}\right.\Rightarrow \left\{\begin{array}{l} M=\left(\dfrac{2x}{\sqrt{2}}+1;0;-\dfrac{2x}{\sqrt{2}}\right)\\ N=\left(\dfrac{3x}{\sqrt{2}};\dfrac{3x}{\sqrt{2}};0\right)\end{array}\right.\Rightarrow \overrightarrow{MN}=\left(\dfrac{x}{\sqrt{2}}-1;-\dfrac{3x}{\sqrt{2}};\dfrac{2x}{\sqrt{2}}\right)$.
Khi đó $MN=\sqrt{\left(\dfrac{x}{\sqrt{2}}-1\right)^2+\left(-\dfrac{3x}{\sqrt{2}}\right)^2+\left(\dfrac{2x}{\sqrt{2}}\right)^2}=\sqrt{7x^2-\sqrt{2}x+1}=f(x)$.
Suy ra $MN_{\min\limits}=f\left(\dfrac{\sqrt{2}}{14}\right)=\sqrt{\dfrac{13}{14}}$.
Vậy khoảng cách ngắn nhất giữa hai chú kiến bằng $20\cdot \sqrt{\dfrac{13}{14}}\approx 19{,}3$ cm.
