Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng nằm ngang

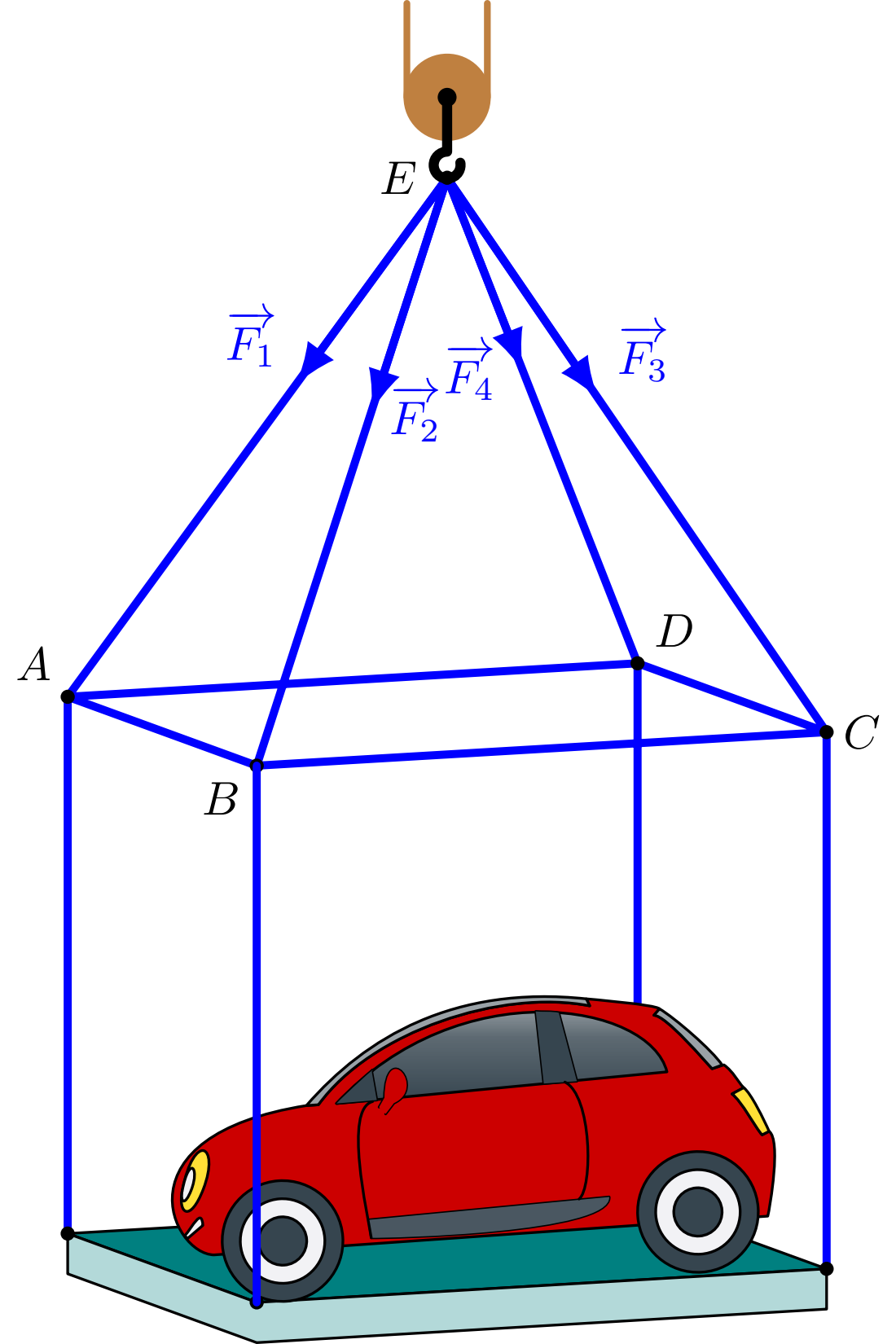
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc $E$ của chiếc cần cẩu sao cho các đoạn dây cáp $EA$, $EB$, $EC$, $ED$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $60^\circ$ (Hình). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng của chiếc xe ô tô (làm tròn đến hàng đơn vị), biết rằng các lực căng $\overrightarrow{F_1}$, $\overrightarrow{F_2}$, $\overrightarrow{F_3}$, $\overrightarrow{F_4}$ đều có độ lớn là $4700$ N và trọng lượng của khung sắt là $3000$ N.

Đáp án: 1328
Lời giải: Gọi $O$ là tâm hình chữ nhật $ABCD$.
Ta có $\widehat{AEC}=60^\circ$ vì $\triangle EAC$ đều.
Và $\overrightarrow{F_1}+\overrightarrow{F_3}=2\overrightarrow{EO}\Rightarrow \left|\overrightarrow{F_1}+\overrightarrow{F_3}\right|=2\left|\overrightarrow{EO}\right|= F_1\sqrt{3}=4700\sqrt{3}$.
Tương tự ta có, $\left|\overrightarrow{F_2}+\overrightarrow{F_4}\right|=\left|\overrightarrow{F_2}\right|\sqrt{3}=4700\sqrt{3}$.
Vậy trọng lực ô tô là $F=\left|\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\overrightarrow{F_4}\right|- 3000\approx 1328$ N.