Một chiếc đèn tròn được treo song song vối mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm $O$ trên trẩn nhà và lẩn lượt buộc vào ba điểm $A$, $B$, $C$ trên đèn tròn sao cho các lực căng $\overrightarrow{F}_1$, $\overrightarrow{F}_2$, $\overrightarrow{F}_3$ lần lượt trên mỗi dây $OA$, $OB$, $OC$ đôi một vuông góc với nhau

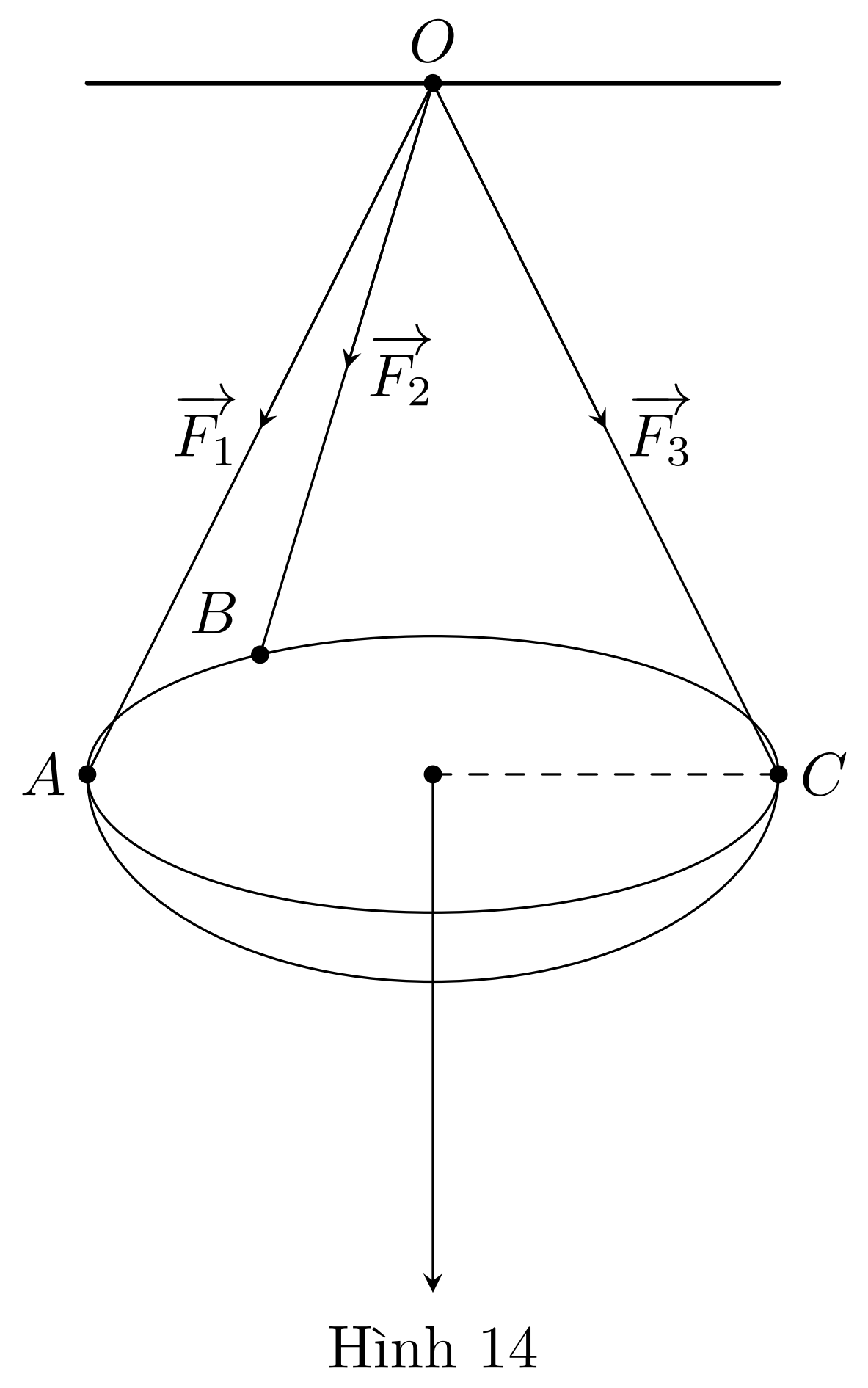
Một chiếc đèn tròn được treo song song vối mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm $O$ trên trẩn nhà và lẩn lượt buộc vào ba điểm $A$, $B$, $C$ trên đèn tròn sao cho các lực căng $\overrightarrow{F}_1$, $\overrightarrow{F}_2$, $\overrightarrow{F}_3$ lần lượt trên mỗi dây $OA$, $OB$, $OC$ đôi một vuông góc với nhau. và $\left|\overrightarrow{F}_1\right|=\left|\overrightarrow{F}_2\right|=\left|\overrightarrow{F_3}\right|=15(\mathrm{~N})$ (Hình 14).
Tính trọng lượng của chiếc đèn tròn đó (làm tròn đến hàng đơn vị).

Đáp án: 26
Lời giải:

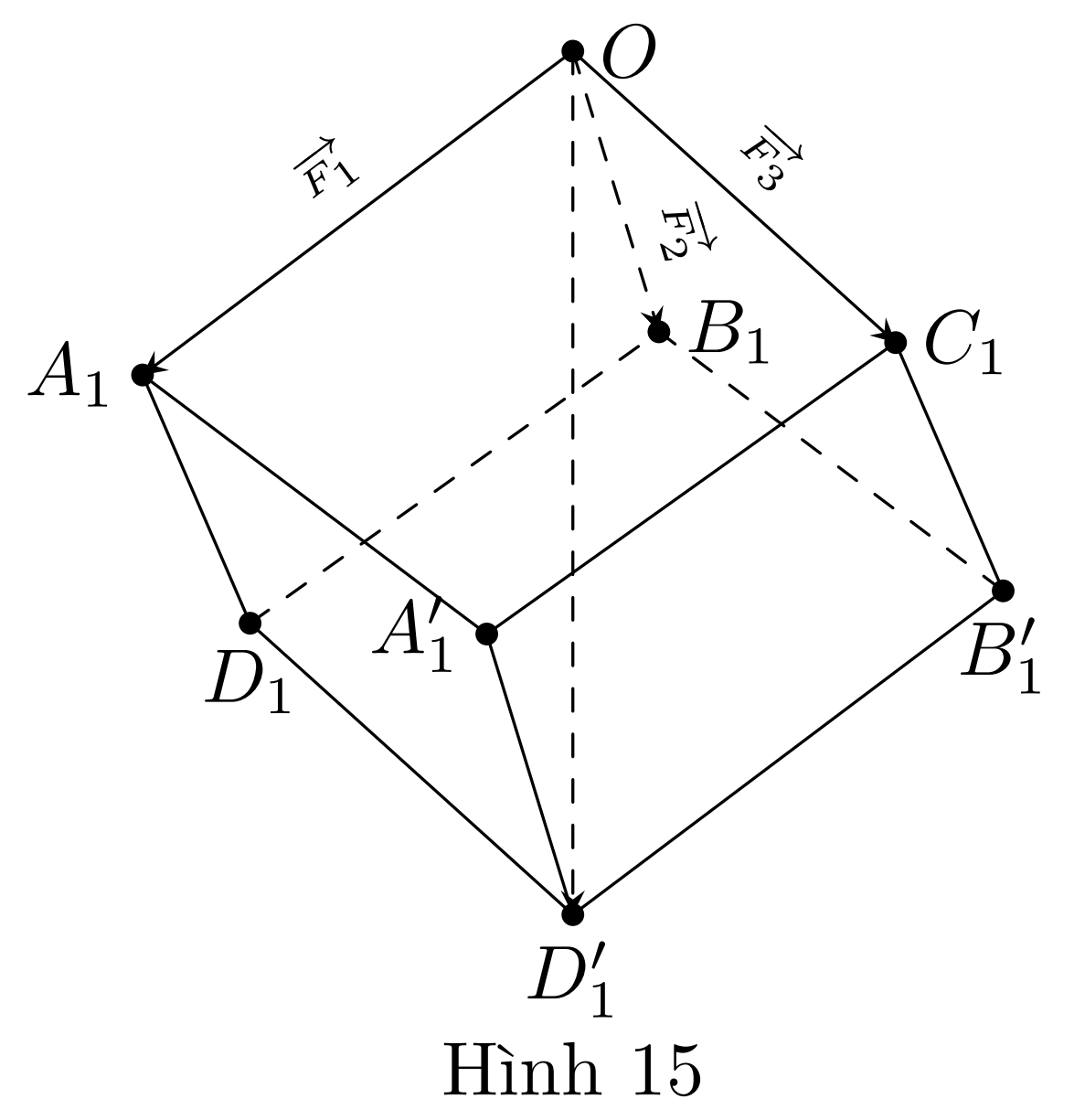
Gọi $A_1$, $B_1$, $C_1$ lần lượt là các điểm sao cho $\overrightarrow{OA_1}=\overrightarrow{F}_1$, $\overrightarrow{OB_1}=\overrightarrow{F_2}$, $\overrightarrow{OC_1}=\overrightarrow{F}_3$. Lấy các điểm $D_1$, $A_1’$, $B_1’$, $D_1’$, sao cho $OA_1D_1B_1\cdot C_1A_1′ D_1′ B_1’$ là hình hộp (Hình 15). Khi đó, áp dụng quy tắc hình hộp, ta có:
$\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC_1}=\overrightarrow{OD’_1} $
Mặt khác, do các lực căng $\overrightarrow{F}_1$, $\overrightarrow{F_2}$, $\overrightarrow{F_3}$ đôi một vuông góc và $\left|\overrightarrow{F}_1\right|=\left|\overrightarrow{F}_2\right|=\left|\overrightarrow{F}_3\right|=15$ (N) nên hình hộp $OA_1D_1B_1. C_1A_1 D_1’B_1’$ có ba cạnh $OA_1$, $OB_1$, $OC_1$ đôi một vuông góc và bằng nhau. Vì thế hình hộp đó là hình lập phương có độ dài cạnh bằng $15$. Suy ra độ dài đường chéo $OD_1’$ của hình lập phương đó bằng $15\sqrt{3}$.
Do chiếc đèn ở vị trí cân bằng nên $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{P}$, ở đó $\overrightarrow{P}$ là trọng lực tác dụng lên chiếc đèn.\\ Suy ra trọng lượng của chiếc đèn là: $\left|\overrightarrow{P}\right|=\left|\overrightarrow{OD_1}\right|=15 \sqrt{3}\approx 26$ (N).